A Differential Invariant for Zooming
Paper and Code
Aug 26, 1999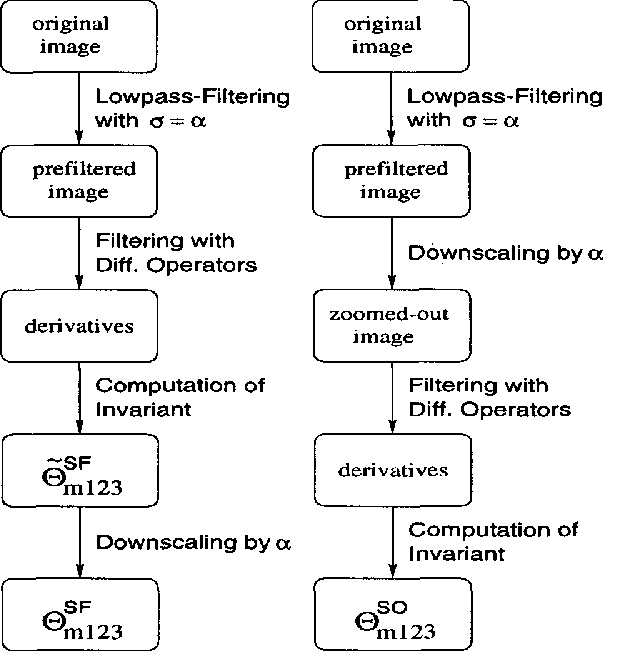
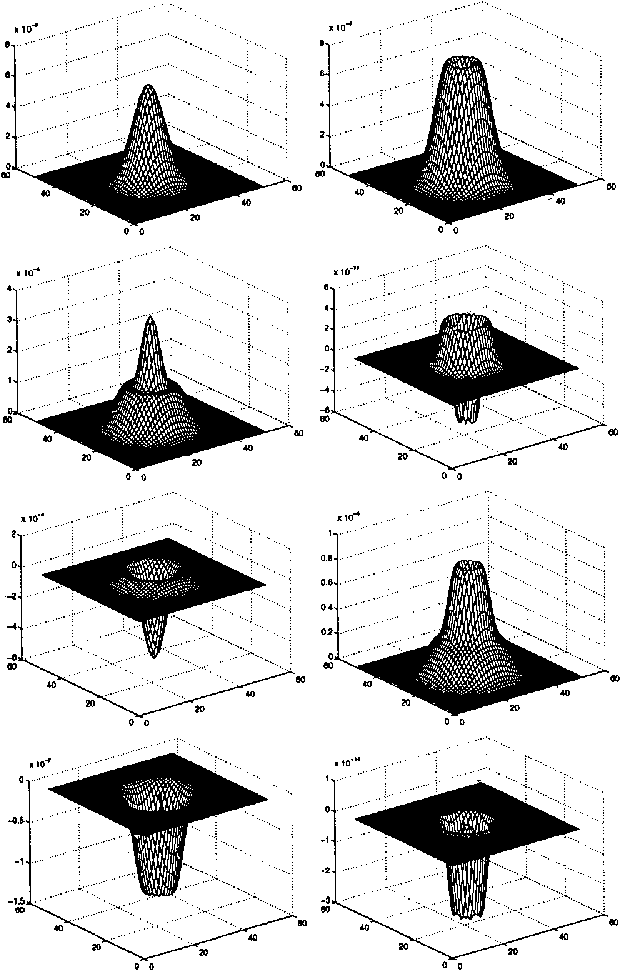
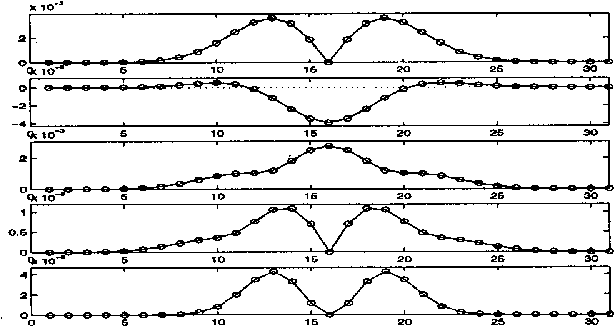
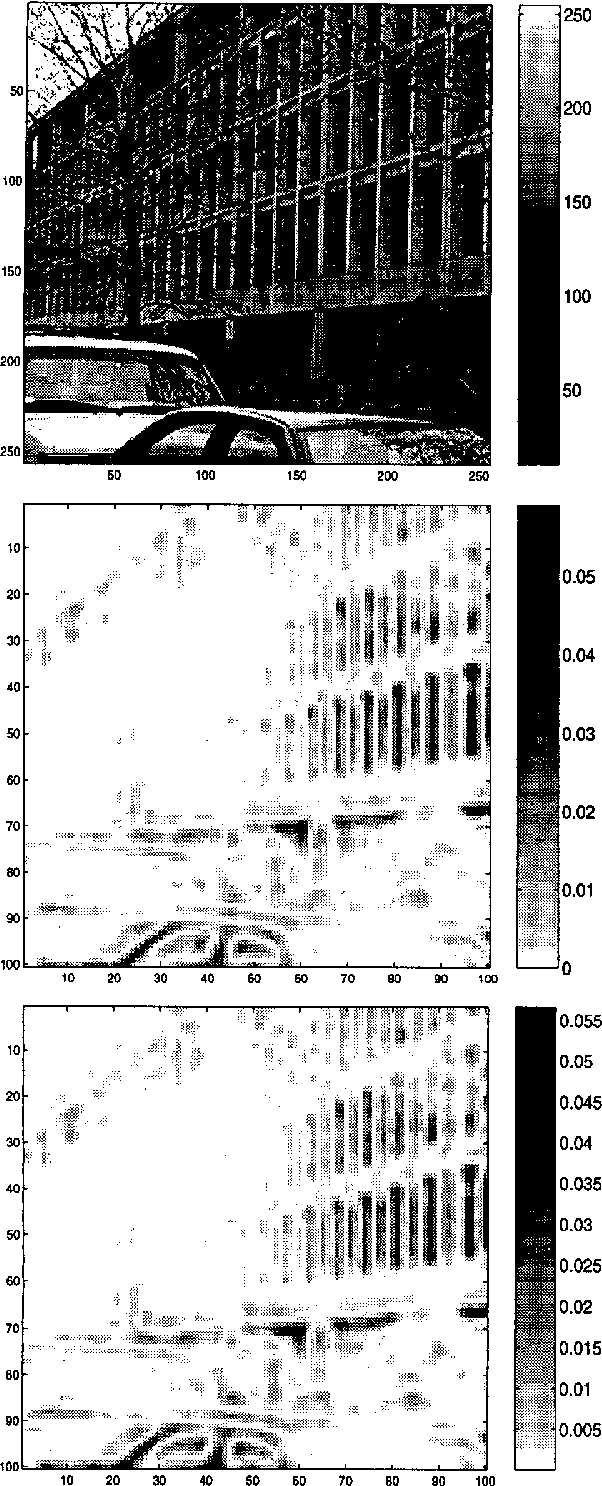
This paper presents an invariant under scaling and linear brightness change. The invariant is based on differentials and therefore is a local feature. Rotationally invariant 2-d differential Gaussian operators up to third order are proposed for the implementation of the invariant. The performance is analyzed by simulating a camera zoom-out.
* Proceedings 1999 International Conference on Image Processing,
Kobe, 25-28 October 1999 * 5 pages, 7 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge