A cusp-capturing PINN for elliptic interface problems
Paper and Code
Oct 16, 2022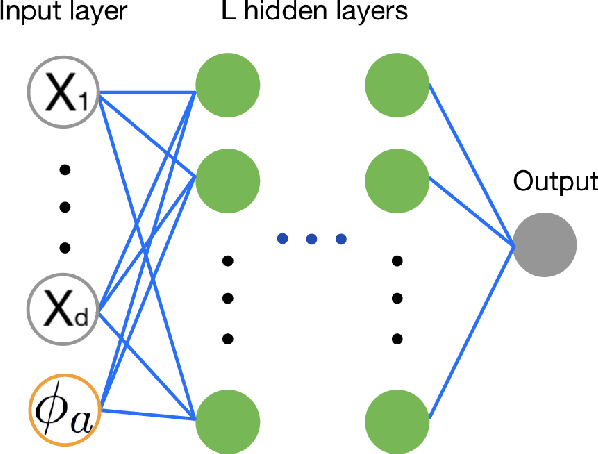

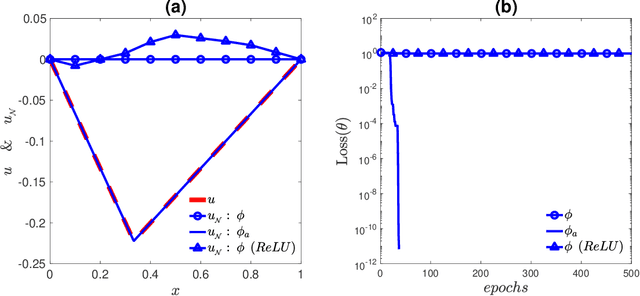

In this paper, we propose a cusp-capturing physics-informed neural network (PINN) to solve variable-coefficient elliptic interface problems whose solution is continuous but has discontinuous first derivatives on the interface. To find such a solution using neural network representation, we introduce a cusp-enforced level set function as an additional feature input to the network to retain the inherent solution properties, capturing the solution cusps (where the derivatives are discontinuous) sharply. In addition, the proposed neural network has the advantage of being mesh-free, so it can easily handle problems in irregular domains. We train the network using the physics-informed framework in which the loss function comprises the residual of the differential equation together with a certain interface and boundary conditions. We conduct a series of numerical experiments to demonstrate the effectiveness of the cusp-capturing technique and the accuracy of the present network model. Numerical results show that even a one-hidden-layer (shallow) network with a moderate number of neurons ($40-60$) and sufficient training data points, the present network model can achieve high prediction accuracy (relative $L^2$ errors in the order of $10^{-5}-10^{-6}$), which outperforms several existing neural network models and traditional grid-based methods in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge