A Convex Optimization Framework for Constrained Concurrent Motion Control of a Hybrid Redundant Surgical System
Paper and Code
Jan 21, 2018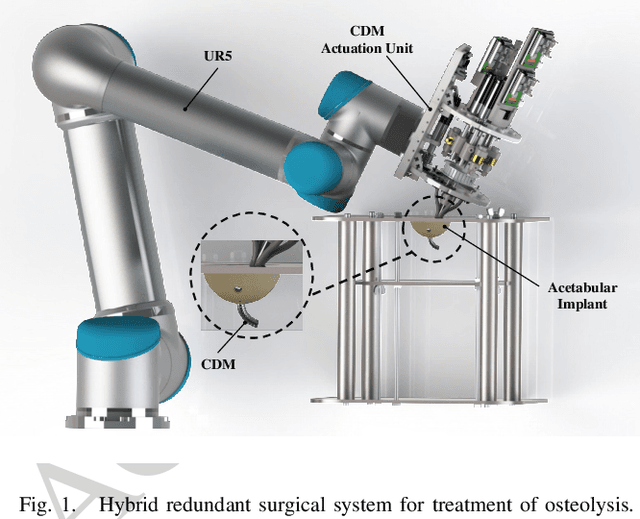
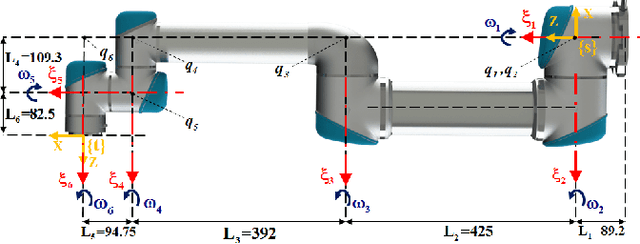
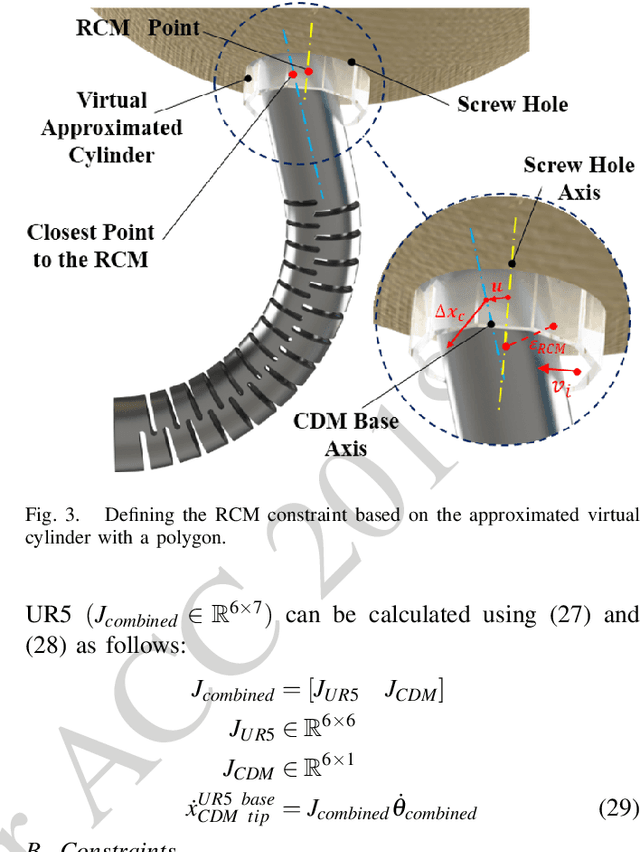
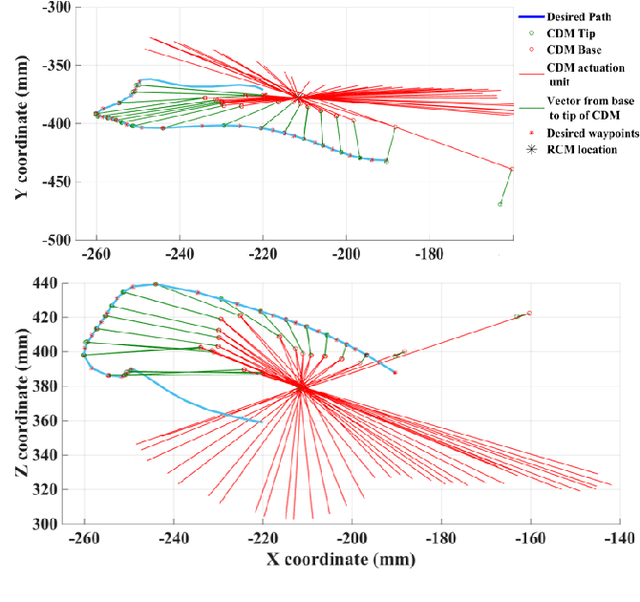
We present a constrained motion control framework for a redundant surgical system designed for minimally invasive treatment of pelvic osteolysis. The framework comprises a kinematics model of a six Degrees-of-Freedom (DoF) robotic arm integrated with a one DoF continuum manipulator as well as a novel convex optimization redundancy resolution controller. To resolve the redundancy resolution problem, formulated as a constrained l2-regularized quadratic minimization, we study and evaluate the potential use of an optimally tuned alternating direction method of multipliers (ADMM) algorithm. To this end, we prove global convergence of the algorithm at linear rate and propose expressions for the involved parameters resulting in a fast convergence. Simulations on the robotic system verified our analytical derivations and showed the capability and robustness of the ADMM algorithm in constrained motion control of our redundant surgical system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge