A convex formulation of covariate-adjusted Gaussian graphical models via natural parametrization
Paper and Code
Oct 08, 2024
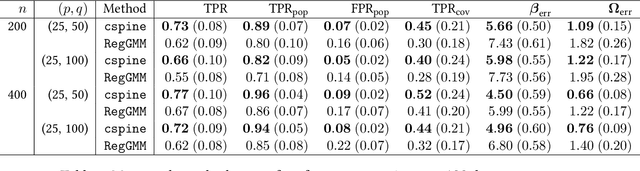

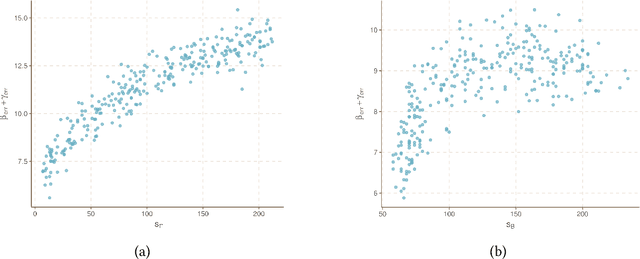
Gaussian graphical models (GGMs) are widely used for recovering the conditional independence structure among random variables. Recently, several key advances have been made to exploit an additional set of variables for better estimating the GGMs of the variables of interest. For example, in co-expression quantitative trait locus (eQTL) studies, both the mean expression level of genes as well as their pairwise conditional independence structure may be adjusted by genetic variants local to those genes. Existing methods to estimate covariate-adjusted GGMs either allow only the mean to depend on covariates or suffer from poor scaling assumptions due to the inherent non-convexity of simultaneously estimating the mean and precision matrix. In this paper, we propose a convex formulation that jointly estimates the covariate-adjusted mean and precision matrix by utilizing the natural parametrization of the multivariate Gaussian likelihood. This convexity yields theoretically better performance as the sparsity and dimension of the covariates grow large relative to the number of samples. We verify our theoretical results with numerical simulations and perform a reanalysis of an eQTL study of glioblastoma multiforme (GBM), an aggressive form of brain cancer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge