A convergence and asymptotic analysis of the generalized symmetric FastICA algorithm

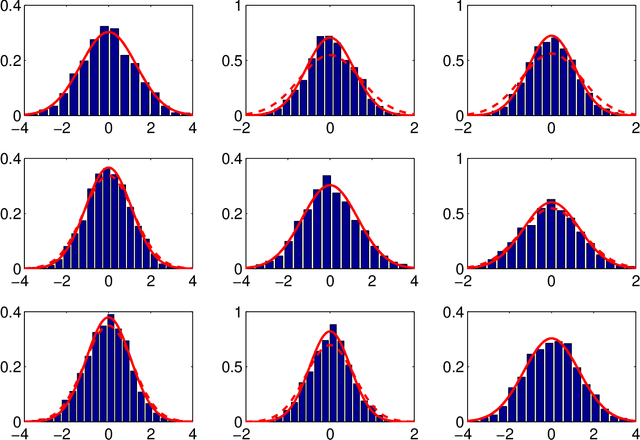
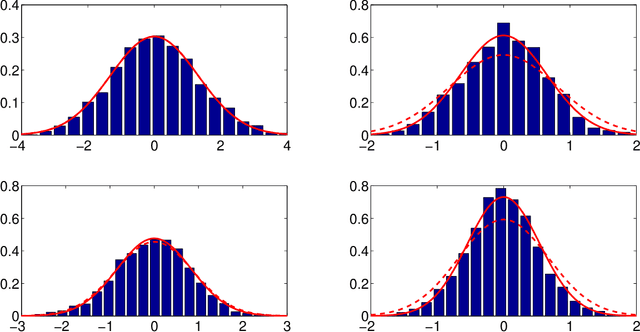
This contribution deals with the generalized symmetric FastICA algorithm in the domain of Independent Component Analysis (ICA). The generalized symmetric version of FastICA has been shown to have the potential to achieve the Cram\'er-Rao Bound (CRB) by allowing the usage of different nonlinearity functions in its parallel implementations of one-unit FastICA. In spite of this appealing property, a rigorous study of the asymptotic error of the generalized symmetric FastICA algorithm is still missing in the community. In fact, all the existing results exhibit certain limitations, such as ignoring the impact of data standardization on the asymptotic statistics or being based on a heuristic approach. In this work, we aim at filling this blank. The first result of this contribution is the characterization of the limits of the generalized symmetric FastICA. It is shown that the algorithm optimizes a function that is a sum of the contrast functions used by traditional one-unit FastICA with a correction of the sign. Based on this characterization, we derive a closed-form analytic expression of the asymptotic covariance matrix of the generalized symmetric FastICA estimator using the method of estimating equation and M-estimator.