A Combinatorial Algebraic Approach for the Identifiability of Low-Rank Matrix Completion

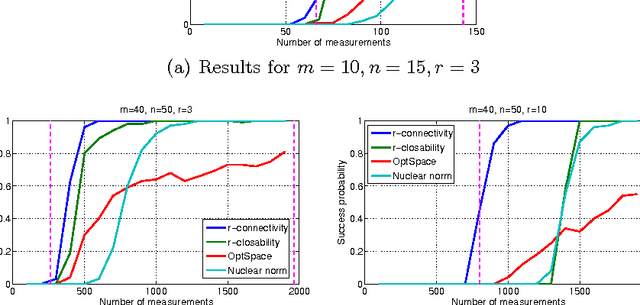
In this paper, we review the problem of matrix completion and expose its intimate relations with algebraic geometry, combinatorics and graph theory. We present the first necessary and sufficient combinatorial conditions for matrices of arbitrary rank to be identifiable from a set of matrix entries, yielding theoretical constraints and new algorithms for the problem of matrix completion. We conclude by algorithmically evaluating the tightness of the given conditions and algorithms for practically relevant matrix sizes, showing that the algebraic-combinatoric approach can lead to improvements over state-of-the-art matrix completion methods.