A Characterization of Semi-Supervised Adversarially-Robust PAC Learnability

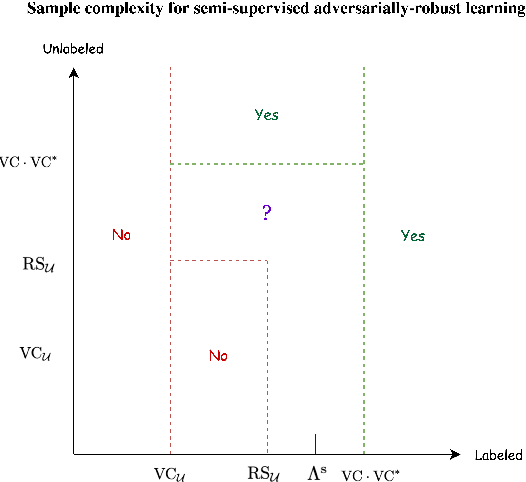
We study the problem of semi-supervised learning of an adversarially-robust predictor in the PAC model, where the learner has access to both labeled and unlabeled examples. The sample complexity in semi-supervised learning has two parameters, the number of labeled examples and the number of unlabeled examples. We consider the complexity measures, $VC_U \leq dim_U \leq VC$ and $VC^*$, where $VC$ is the standard $VC$-dimension, $VC^*$ is its dual, and the other two measures appeared in Montasser et al. (2019). The best sample bound known for robust supervised PAC learning is $O(VC \cdot VC^*)$, and we will compare our sample bounds to $\Lambda$ which is the minimal number of labeled examples required by any robust supervised PAC learning algorithm. Our main results are the following: (1) in the realizable setting it is sufficient to have $O(VC_U)$ labeled examples and $O(\Lambda)$ unlabeled examples. (2) In the agnostic setting, let $\eta$ be the minimal agnostic error. The sample complexity depends on the resulting error rate. If we allow an error of $2\eta+\epsilon$, it is still sufficient to have $O(VC_U)$ labeled examples and $O(\Lambda)$ unlabeled examples. If we insist on having an error $\eta+\epsilon$ then $\Omega(dim_U)$ labeled examples are necessary, as in the supervised case. The above results show that there is a significant benefit in semi-supervised robust learning, as there are hypothesis classes with $VC_U=0$ and $dim_U$ arbitrary large. In supervised learning, having access only to labeled examples requires at least $\Lambda \geq dim_U$ labeled examples. Semi-supervised require only $O(1)$ labeled examples and $O(\Lambda)$ unlabeled examples. A byproduct of our result is that if we assume that the distribution is robustly realizable by a hypothesis class, then with respect to the 0-1 loss we can learn with only $O(VC_U)$ labeled examples, even if the $VC$ is infinite.