A case where a spindly two-layer linear network whips any neural network with a fully connected input layer
Paper and Code
Oct 16, 2020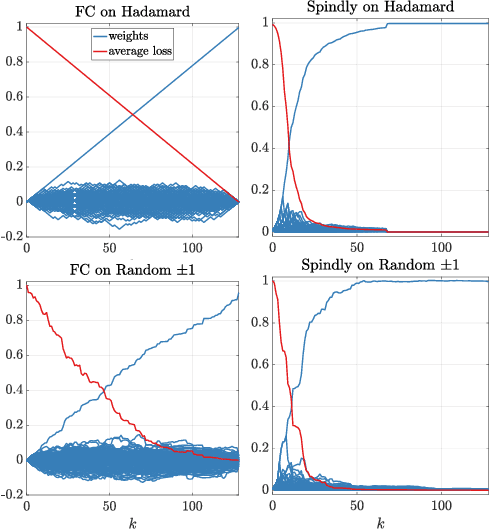
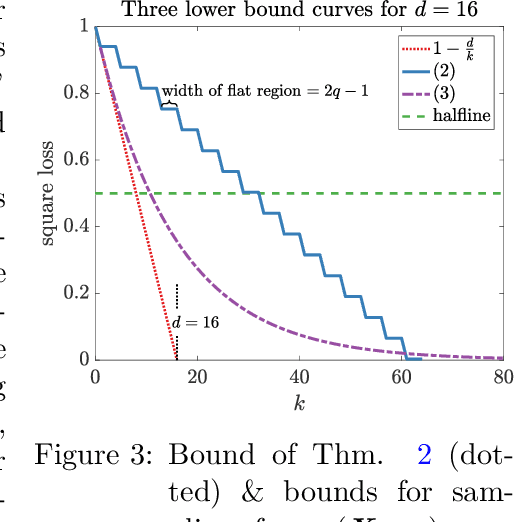
It was conjectured that any neural network of any structure and arbitrary differentiable transfer functions at the nodes cannot learn the following problem sample efficiently when trained with gradient descent: The instances are the rows of a $d$-dimensional Hadamard matrix and the target is one of the features, i.e. very sparse. We essentially prove this conjecture: We show that after receiving a random training set of size $k < d$, the expected square loss is still $1-\frac{k}{(d-1)}$. The only requirement needed is that the input layer is fully connected and the initial weight vectors of the input nodes are chosen from a rotation invariant distribution. Surprisingly the same type of problem can be solved drastically more efficient by a simple 2-layer linear neural network in which the $d$ inputs are connected to the output node by chains of length 2 (Now the input layer has only one edge per input). When such a network is trained by gradient descent, then it has been shown that its expected square loss is $\frac{\log d}{k}$. Our lower bounds essentially show that a sparse input layer is needed to sample efficiently learn sparse targets with gradient descent when the number of examples is less than the number of input features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge