A Capacity Scaling Law for Artificial Neural Networks
Paper and Code
Sep 10, 2018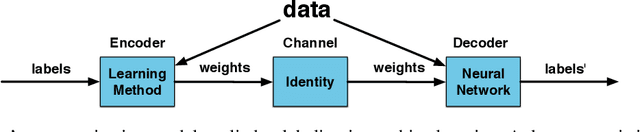
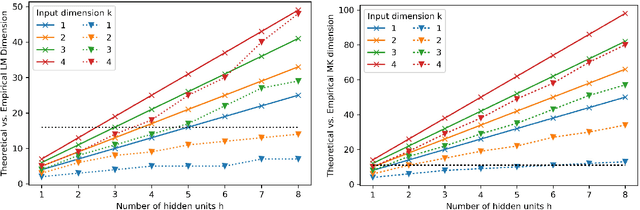
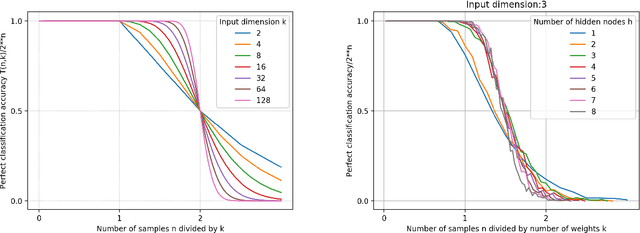
We derive the calculation of two critical numbers predicting the behavior of perceptron networks. First, we derive the calculation of what we call the lossless memory (LM) dimension. The LM dimension is a generalization of the Vapnik--Chervonenkis (VC) dimension that avoids structured data and therefore provides an upper bound for perfectly fitting almost any training data. Second, we derive what we call the MacKay (MK) dimension. This limit indicates a 50% chance of not being able to train a given function. Our derivations are performed by embedding a neural network into Shannon's communication model which allows to interpret the two points as capacities measured in bits. We present a proof and practical experiments that validate our upper bounds with repeatable experiments using different network configurations, diverse implementations, varying activation functions, and several learning algorithms. The bottom line is that the two capacity points scale strictly linear with the number of weights. Among other practical applications, our result allows to compare and benchmark different neural network implementations independent of a concrete learning task. Our results provide insight into the capabilities and limits of neural networks and generate valuable know how for experimental design decisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge