A Broad Class of Discrete-Time Hypercomplex-Valued Hopfield Neural Networks

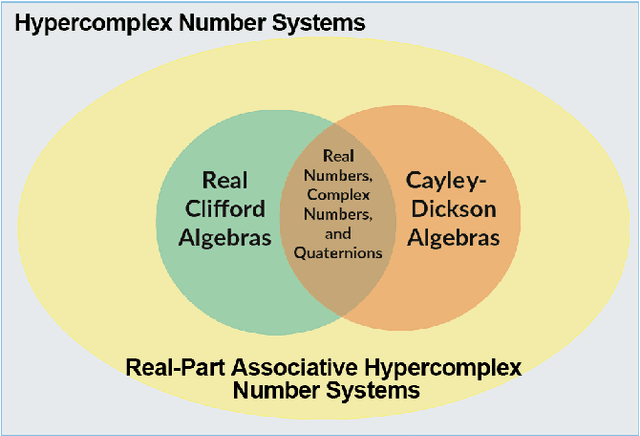
In this paper, we address the stability of a broad class of discrete-time hypercomplex-valued Hopfield-type neural networks. To ensure the neural networks belonging to this class always settle down at a stationary state, we introduce novel hypercomplex number systems referred to as Hopfield-type hypercomplex number systems. Hopfield-type hypercomplex number systems generalize the well-known Cayley-Dickson algebras and real Clifford algebras and include the systems of real numbers, complex numbers, dual numbers, hyperbolic numbers, quaternions, tessarines, and octonions as particular instances. Apart from the novel hypercomplex number systems, we introduce a family of hypercomplex-valued activation functions called Hopfield-type activation functions. Broadly speaking, a Hopfield-type activation function projects the activation potential onto the set of all possible states of a hypercomplex-valued neuron. Using the theory presented in this paper, we confirm the stability analysis of several discrete-time hypercomplex-valued Hopfield-type neural networks from the literature. Moreover, we introduce and provide the stability analysis of a general class of Hopfield-type neural networks on Cayley-Dickson algebras.