A Bipartite Graph Neural Network Approach for Scalable Beamforming Optimization
Paper and Code
Jul 12, 2022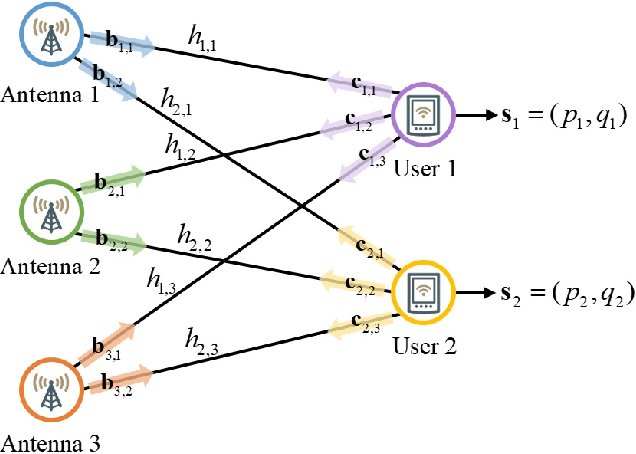
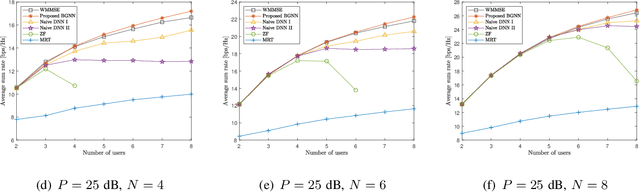
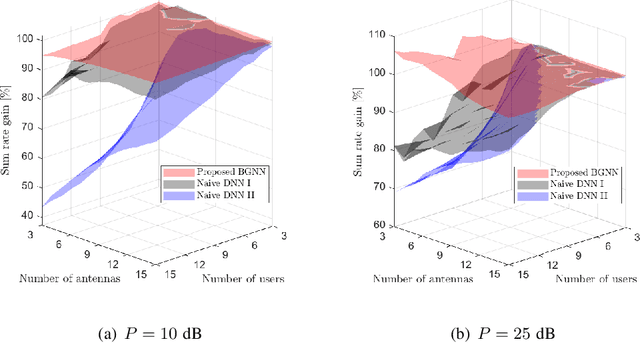
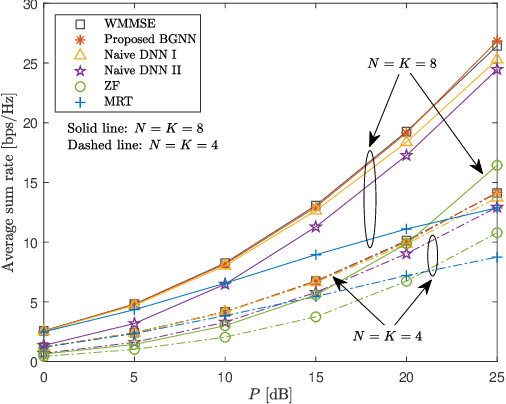
Deep learning (DL) techniques have been intensively studied for the optimization of multi-user multiple-input single-output (MU-MISO) downlink systems owing to the capability of handling nonconvex formulations. However, the fixed computation structure of existing deep neural networks (DNNs) lacks flexibility with respect to the system size, i.e., the number of antennas or users. This paper develops a bipartite graph neural network (BGNN) framework, a scalable DL solution designed for multi-antenna beamforming optimization. The MU-MISO system is first characterized by a bipartite graph where two disjoint vertex sets, each of which consists of transmit antennas and users, are connected via pairwise edges. These vertex interconnection states are modeled by channel fading coefficients. Thus, a generic beamforming optimization process is interpreted as a computation task over a weight bipartite graph. This approach partitions the beamforming optimization procedure into multiple suboperations dedicated to individual antenna vertices and user vertices. Separated vertex operations lead to scalable beamforming calculations that are invariant to the system size. The vertex operations are realized by a group of DNN modules that collectively form the BGNN architecture. Identical DNNs are reused at all antennas and users so that the resultant learning structure becomes flexible to the network size. Component DNNs of the BGNN are trained jointly over numerous MU-MISO configurations with randomly varying network sizes. As a result, the trained BGNN can be universally applied to arbitrary MU-MISO systems. Numerical results validate the advantages of the BGNN framework over conventional methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge