A Better Alternative to Piecewise Linear Time Series Segmentation
Paper and Code
Apr 28, 2007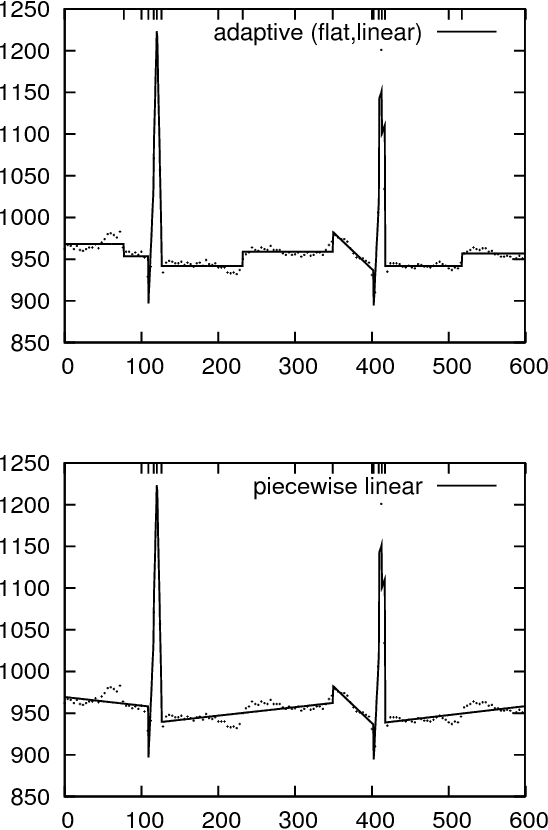
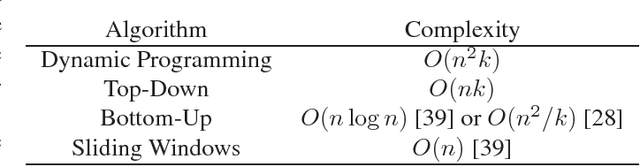
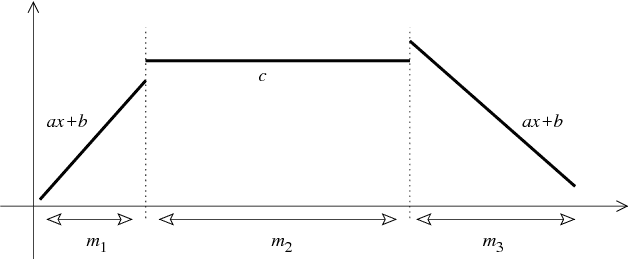
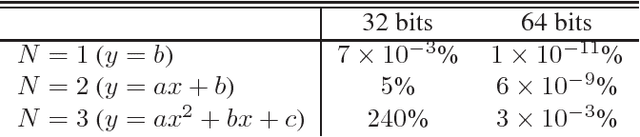
Time series are difficult to monitor, summarize and predict. Segmentation organizes time series into few intervals having uniform characteristics (flatness, linearity, modality, monotonicity and so on). For scalability, we require fast linear time algorithms. The popular piecewise linear model can determine where the data goes up or down and at what rate. Unfortunately, when the data does not follow a linear model, the computation of the local slope creates overfitting. We propose an adaptive time series model where the polynomial degree of each interval vary (constant, linear and so on). Given a number of regressors, the cost of each interval is its polynomial degree: constant intervals cost 1 regressor, linear intervals cost 2 regressors, and so on. Our goal is to minimize the Euclidean (l_2) error for a given model complexity. Experimentally, we investigate the model where intervals can be either constant or linear. Over synthetic random walks, historical stock market prices, and electrocardiograms, the adaptive model provides a more accurate segmentation than the piecewise linear model without increasing the cross-validation error or the running time, while providing a richer vocabulary to applications. Implementation issues, such as numerical stability and real-world performance, are discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge