A Bayes consistent 1-NN classifier
Paper and Code
Aug 17, 2018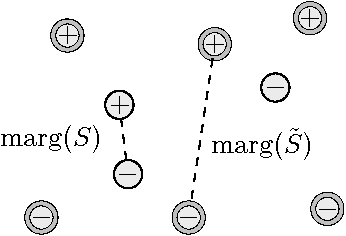

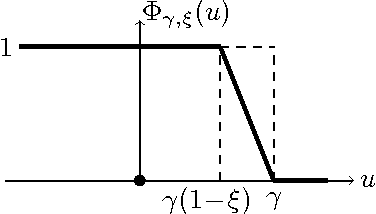
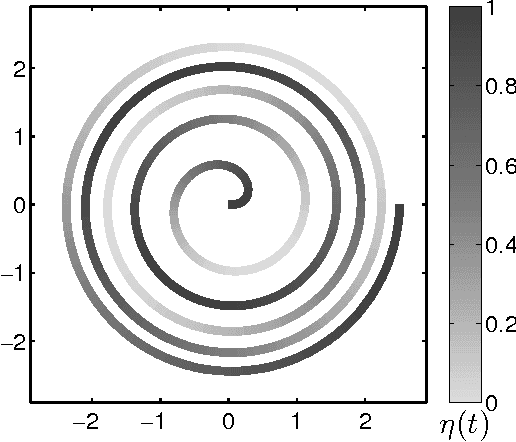
We show that a simple modification of the 1-nearest neighbor classifier yields a strongly Bayes consistent learner. Prior to this work, the only strongly Bayes consistent proximity-based method was the k-nearest neighbor classifier, for k growing appropriately with sample size. We will argue that a margin-regularized 1-NN enjoys considerable statistical and algorithmic advantages over the k-NN classifier. These include user-friendly finite-sample error bounds, as well as time- and memory-efficient learning and test-point evaluation algorithms with a principled speed-accuracy tradeoff. Encouraging empirical results are reported.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge