A Basic Compositional Model for Spiking Neural Networks
Paper and Code
Aug 12, 2018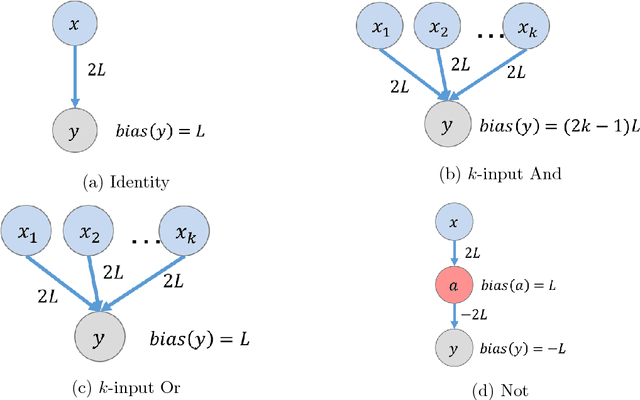
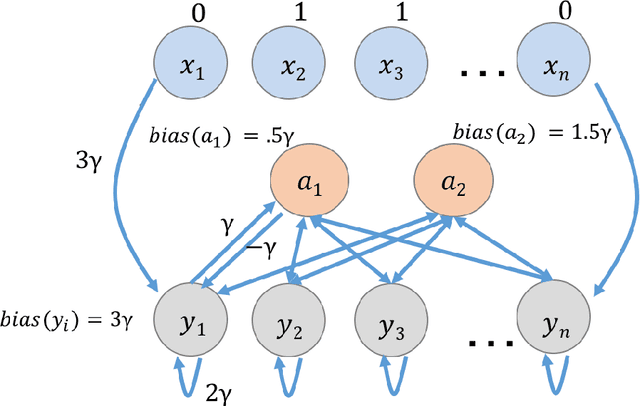
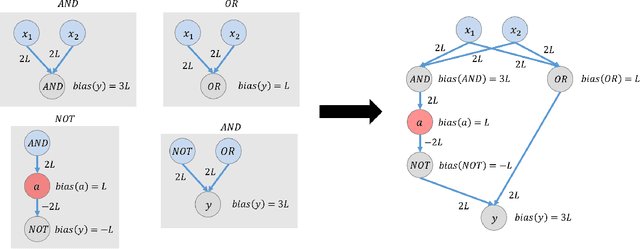
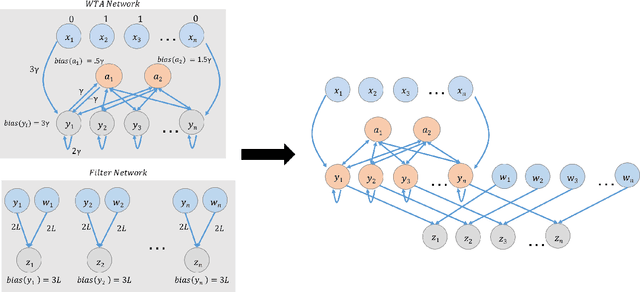
This paper is part of a project on developing an algorithmic theory of brain networks, based on stochastic Spiking Neural Network (SNN) models. Inspired by tasks that seem to be solved in actual brains, we are defining abstract problems to be solved by these networks. In our work so far, we have developed models and algorithms for the Winner-Take-All problem from computational neuroscience [LMP17a,Mus18], and problems of similarity detection and neural coding [LMP17b]. We plan to consider many other problems and networks, including both static networks and networks that learn. This paper is about basic theory for the stochastic SNN model. In particular, we define a simple version of the model. This version assumes that the neurons' only state is a Boolean, indicating whether the neuron is firing or not. In later work, we plan to develop variants of the model with more elaborate state. We also define an external behavior notion for SNNs, which can be used for stating requirements to be satisfied by the networks. We then define a composition operator for SNNs. We prove that our external behavior notion is "compositional", in the sense that the external behavior of a composed network depends only on the external behaviors of the component networks. We also define a hiding operator that reclassifies some output behavior of an SNN as internal. We give basic results for hiding. Finally, we give a formal definition of a problem to be solved by an SNN, and give basic results showing how composition and hiding of networks affect the problems that they solve. We illustrate our definitions with three examples: building a circuit out of gates, building an "Attention" network out of a "Winner-Take-All" network and a "Filter" network, and a toy example involving combining two networks in a cyclic fashion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge