Xiaodong Qi
Gödel's Sentence Is An Adversarial Example But Unsolvable
Feb 25, 2020
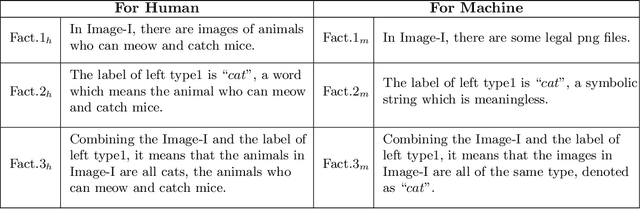


Abstract:In recent years, different types of adversarial examples from different fields have emerged endlessly, including purely natural ones without perturbations. A variety of defenses are proposed and then broken quickly. Two fundamental questions need to be asked: What's the reason for the existence of adversarial examples and are adversarial examples unsolvable? In this paper, we will show the reason for the existence of adversarial examples is there are non-isomorphic natural explanations that can all explain data set. Specifically, for two natural explanations of being true and provable, G\"odel's sentence is an adversarial example but ineliminable. It can't be solved by the re-accumulation of data set or the re-improvement of learning algorithm. Finally, from the perspective of computability, we will prove the incomputability for adversarial examples, which are unrecognizable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge