Smoothness Analysis for Probabilistic Programs with Application to Optimised Variational Inference

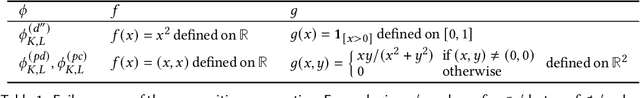
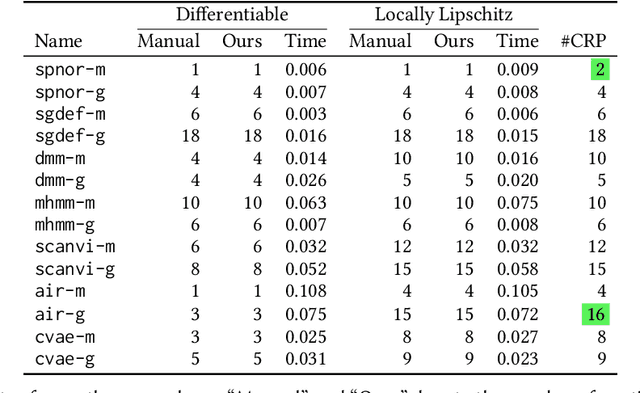
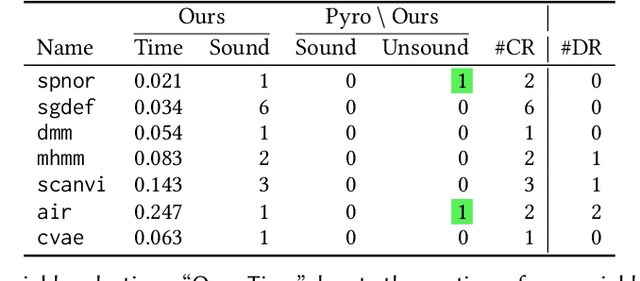
We present a static analysis for discovering differentiable or more generally smooth parts of a given probabilistic program, and show how the analysis can be used to improve the pathwise gradient estimator, one of the most popular methods for posterior inference and model learning. Our improvement increases the scope of the estimator from differentiable models to non-differentiable ones without requiring manual intervention of the user; the improved estimator automatically identifies differentiable parts of a given probabilistic program using our static analysis, and applies the pathwise gradient estimator to the identified parts while using a more general but less efficient estimator, called score estimator, for the rest of the program. Our analysis has a surprisingly subtle soundness argument, partly due to the misbehaviours of some target smoothness properties when viewed from the perspective of program analysis designers. For instance, some smoothness properties are not preserved by function composition, and this makes it difficult to analyse sequential composition soundly without heavily sacrificing precision. We formulate five assumptions on a target smoothness property, prove the soundness of our analysis under those assumptions, and show that our leading examples satisfy these assumptions. We also show that by using information from our analysis, our improved gradient estimator satisfies an important differentiability requirement and thus, under a mild regularity condition, computes the correct estimate on average, i.e., it returns an unbiased estimate. Our experiments with representative probabilistic programs in the Pyro language show that our static analysis is capable of identifying smooth parts of those programs accurately, and making our improved pathwise gradient estimator exploit all the opportunities for high performance in those programs.

On Correctness of Automatic Differentiation for Non-Differentiable Functions

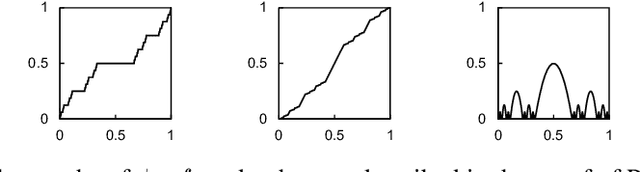
Differentiation lies at the core of many machine-learning algorithms, and is well-supported by popular autodiff systems, such as TensorFlow and PyTorch. Originally, these systems have been developed to compute derivatives of differentiable functions, but in practice, they are commonly applied to functions with non-differentiabilities. For instance, neural networks using ReLU define non-differentiable functions in general, but the gradients of losses involving those functions are computed using autodiff systems in practice. This status quo raises a natural question: are autodiff systems correct in any formal sense when they are applied to such non-differentiable functions? In this paper, we provide a positive answer to this question. Using counterexamples, we first point out flaws in often-used informal arguments, such as: non-differentiabilities arising in deep learning do not cause any issues because they form a measure-zero set. We then investigate a class of functions, called PAP functions, that includes nearly all (possibly non-differentiable) functions in deep learning nowadays. For these PAP functions, we propose a new type of derivatives, called intensional derivatives, and prove that these derivatives always exist and coincide with standard derivatives for almost all inputs. We also show that these intensional derivatives are what most autodiff systems compute or try to compute essentially. In this way, we formally establish the correctness of autodiff systems applied to non-differentiable functions.

Towards Verified Stochastic Variational Inference for Probabilistic Programs

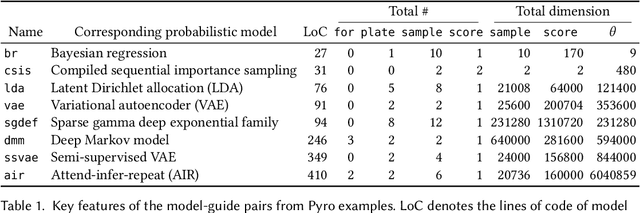
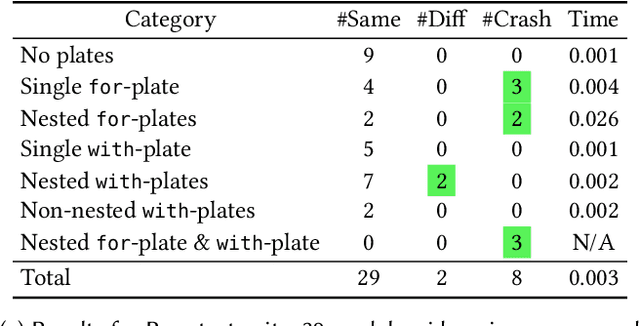
Probabilistic programming is the idea of writing models from statistics and machine learning using program notations and reasoning about these models using generic inference engines. Recently its combination with deep learning has been explored intensely, which led to the development of deep probabilistic programming languages. At the core of this development lie inference engines based on stochastic variational inference algorithms. When asked to find information about the posterior distribution of a model written in such a language, these algorithms convert this posterior-inference query into an optimisation problem and solve it approximately by a form of gradient ascent or descent. In this paper, we analyse one of the most fundamental and versatile variational inference algorithms, called score estimator or REINFORCE, using tools from denotational semantics and program analysis. We formally express what this algorithm does on models denoted by programs, and expose implicit assumptions made by the algorithm on the models. The violation of these assumptions may lead to an undefined optimisation objective or the loss of convergence guarantee of the optimisation process. We then describe rules for proving these assumptions, which can be automated by static program analyses. Some of our rules use nontrivial facts from continuous mathematics, and let us replace requirements about integrals in the assumptions, by conditions involving differentiation or boundedness, which are much easier to prove automatically. Following our general methodology, we have developed a static program analysis for the Pyro programming language that aims at discharging the assumption about what we call model-guide support match. Applied to the eight representative model-guide pairs from the Pyro webpage, our analysis finds a bug in two of these cases and shows that the assumptions are met in the others.