Storing overlapping associative memories on latent manifolds in low-rank spiking networks

Associative memory architectures such as the Hopfield network have long been important conceptual and theoretical models for neuroscience and artificial intelligence. However, translating these abstract models into spiking neural networks has been surprisingly difficult. Indeed, much previous work has been restricted to storing a small number of primarily non-overlapping memories in large networks, thereby limiting their scalability. Here, we revisit the associative memory problem in light of recent advances in understanding spike-based computation. Using a recently-established geometric framework, we show that the spiking activity for a large class of all-inhibitory networks is situated on a low-dimensional, convex, and piecewise-linear manifold, with dynamics that move along the manifold. We then map the associative memory problem onto these dynamics, and demonstrate how the vertices of a hypercubic manifold can be used to store stable, overlapping activity patterns with a direct correspondence to the original Hopfield model. We propose several learning rules, and demonstrate a linear scaling of the storage capacity with the number of neurons, as well as robust pattern completion abilities. Overall, this work serves as a case study to demonstrate the effectiveness of using a geometrical perspective to design dynamics on neural manifolds, with implications for neuroscience and machine learning.

Approximating nonlinear functions with latent boundaries in low-rank excitatory-inhibitory spiking networks

Deep feedforward and recurrent rate-based neural networks have become successful functional models of the brain, but they neglect obvious biological details such as spikes and Dale's law. Here we argue that these details are crucial in order to understand how real neural circuits operate. Towards this aim, we put forth a new framework for spike-based computation in low-rank excitatory-inhibitory spiking networks. By considering populations with rank-1 connectivity, we cast each neuron's spiking threshold as a boundary in a low-dimensional input-output space. We then show how the combined thresholds of a population of inhibitory neurons form a stable boundary in this space, and those of a population of excitatory neurons form an unstable boundary. Combining the two boundaries results in a rank-2 excitatory-inhibitory (EI) network with inhibition-stabilized dynamics at the intersection of the two boundaries. The computation of the resulting networks can be understood as the difference of two convex functions, and is thereby capable of approximating arbitrary non-linear input-output mappings. We demonstrate several properties of these networks, including noise suppression and amplification, irregular activity and synaptic balance, as well as how they relate to rate network dynamics in the limit that the boundary becomes soft. Finally, while our work focuses on small networks (5-50 neurons), we discuss potential avenues for scaling up to much larger networks. Overall, our work proposes a new perspective on spiking networks that may serve as a starting point for a mechanistic understanding of biological spike-based computation.

Biological credit assignment through dynamic inversion of feedforward networks

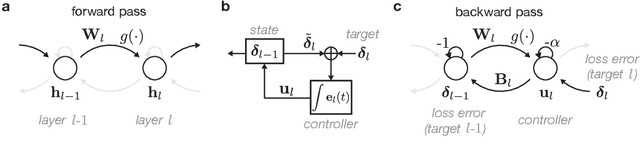
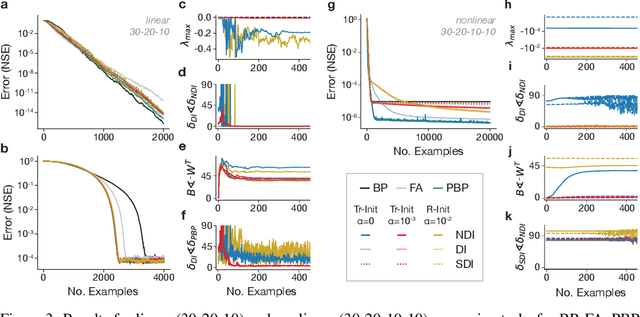
Learning depends on changes in synaptic connections deep inside the brain. In multilayer networks, these changes are triggered by error signals fed back from the output, generally through a stepwise inversion of the feedforward processing steps. The gold standard for this process -- backpropagation -- works well in artificial neural networks, but is biologically implausible. Several recent proposals have emerged to address this problem, but many of these biologically-plausible schemes are based on learning an independent set of feedback connections. This complicates the assignment of errors to each synapse by making it dependent upon a second learning problem, and by fitting inversions rather than guaranteeing them. Here, we show that feedforward network transformations can be effectively inverted through dynamics. We derive this dynamic inversion from the perspective of feedback control, where the forward transformation is reused and dynamically interacts with fixed or random feedback to propagate error signals during the backward pass. Importantly, this scheme does not rely upon a second learning problem for feedback because accurate inversion is guaranteed through the network dynamics. We map these dynamics onto generic feedforward networks, and show that the resulting algorithm performs well on several supervised and unsupervised datasets. We also link this dynamic inversion to Gauss-Newton optimization, suggesting a biologically-plausible approximation to second-order learning. Overall, our work introduces an alternative perspective on credit assignment in the brain, and proposes a special role for temporal dynamics and feedback control during learning.