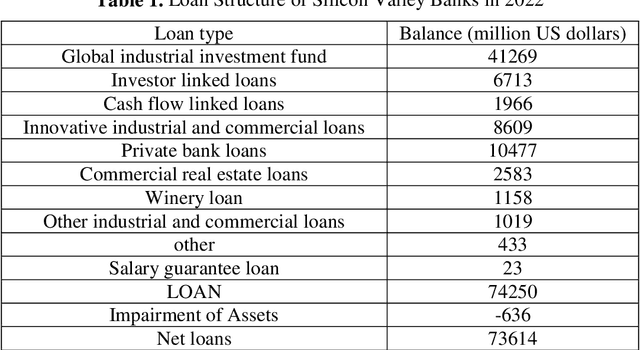
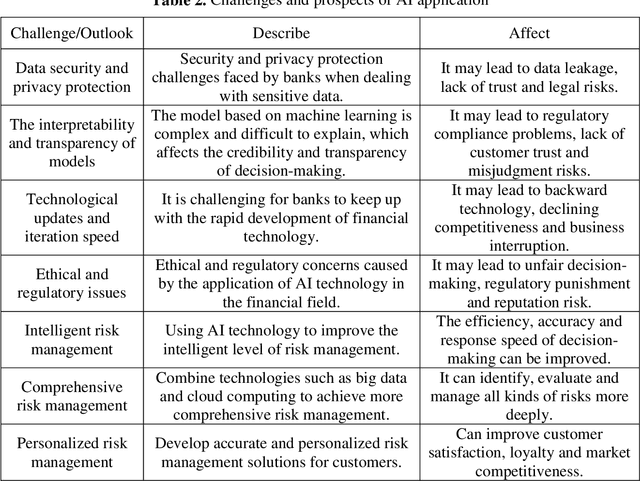
Innovative Application of Artificial Intelligence Technology in Bank Credit Risk Management

With the rapid growth of technology, especially the widespread application of artificial intelligence (AI) technology, the risk management level of commercial banks is constantly reaching new heights. In the current wave of digitalization, AI has become a key driving force for the strategic transformation of financial institutions, especially the banking industry. For commercial banks, the stability and safety of asset quality are crucial, which directly relates to the long-term stable growth of the bank. Among them, credit risk management is particularly core because it involves the flow of a large amount of funds and the accuracy of credit decisions. Therefore, establishing a scientific and effective credit risk decision-making mechanism is of great strategic significance for commercial banks. In this context, the innovative application of AI technology has brought revolutionary changes to bank credit risk management. Through deep learning and big data analysis, AI can accurately evaluate the credit status of borrowers, timely identify potential risks, and provide banks with more accurate and comprehensive credit decision support. At the same time, AI can also achieve realtime monitoring and early warning, helping banks intervene before risks occur and reduce losses.

A General Framework of Multi-Armed Bandit Processes by Arm Switch Restrictions

This paper proposes a general framework of multi-armed bandit (MAB) processes by introducing a type of restrictions on the switches among arms evolving in continuous time. The Gittins index process is constructed for any single arm subject to the restrictions on switches and then the optimality of the corresponding Gittins index rule is established. The Gittins indices defined in this paper are consistent with the ones for MAB processes in continuous time, integer time, semi-Markovian setting as well as general discrete time setting, so that the new theory covers the classical models as special cases and also applies to many other situations that have not yet been touched in the literature. While the proof of the optimality of Gittins index policies benefits from ideas in the existing theory of MAB processes in continuous time, new techniques are introduced which drastically simplify the proof.