Analysis of Partially-Calibrated Sparse Subarrays for Direction Finding with Extended Degrees of Freedom

This paper investigates the problem of direction-of-arrival (DOA) estimation using multiple partially-calibrated sparse subarrays. In particular, we present the Generalized Coarray Multiple Signal Classification (GCA-MUSIC) DOA estimation algorithm to scenarios with partially-calibrated sparse subarrays. The proposed GCA-MUSIC algorithm exploits the difference coarray for each subarray, followed by a specific pseudo-spectrum merging rule that is based on the intersection of the signal subspaces associated to each subarray. This rule assumes that there is no a priori knowledge about the cross-covariance between subarrays. In that way, only the second-order statistics of each subarray are used to estimate the directions with increased degrees of freedom, i.e., the estimation procedure preserves the coarray Multiple Signal Classification and sparse arrays properties to estimate more sources than the number of physical sensors in each subarray. Numerical simulations show that the proposed GCA-MUSIC has better performance than other similar strategies.

Study of List-Based OMP and an Enhanced Model for Direction Finding with Non-Uniform Arrays

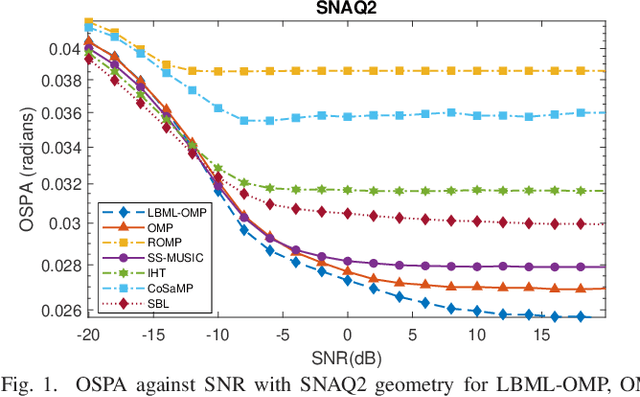
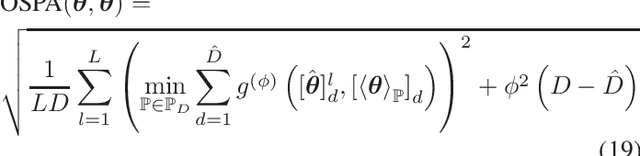
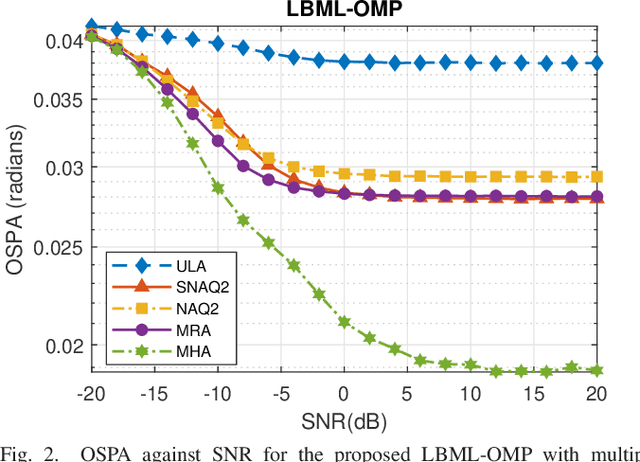
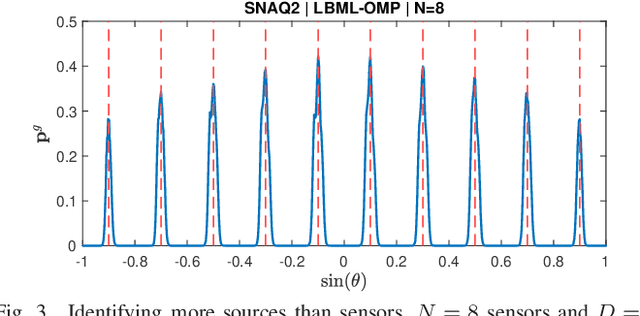
This paper proposes an enhanced coarray transformation model (EDCTM) and a mixed greedy maximum likelihood algorithm called List-Based Maximum Likelihood Orthogonal Matching Pursuit (LBML-OMP) for direction-of-arrival estimation with non-uniform linear arrays (NLAs). The proposed EDCTM approach obtains improved estimates when Khatri-Rao product-based models are used to generate difference coarrays under the assumption of uncorrelated sources. In the proposed LBML-OMP technique, for each iteration a set of candidates is generated based on the correlation-maximization between the dictionary and the residue vector. LBML-OMP then chooses the best candidate based on a reduced-complexity asymptotic maximum likelihood decision rule. Simulations show the improved results of EDCTM over existing approaches and that LBML-OMP outperforms existing sparse recovery algorithms as well as Spatial Smoothing Multiple Signal Classification with NLAs.