Vsevolod Nikulin
Initialization of Latent Space Coordinates via Random Linear Projections for Learning Robotic Sensory-Motor Sequences
Feb 26, 2022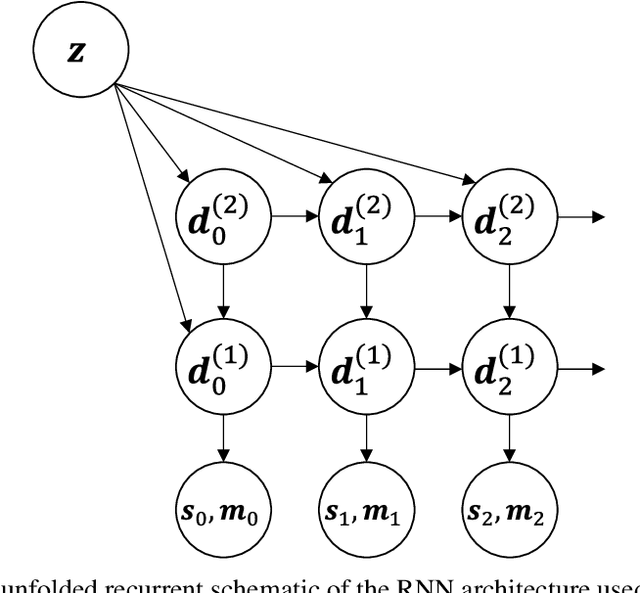


Abstract:Robot kinematics data, despite being a high dimensional process, is highly correlated, especially when considering motions grouped in certain primitives. These almost linear correlations within primitives allow us to interpret the motions as points drawn close to a union of low-dimensional linear subspaces in the space of all motions. Motivated by results of embedding theory, in particular, generalizations of Whitney embedding theorem, we show that random linear projection of motor sequences into low dimensional space loses very little information about structure of kinematics data. Projected points are very good initial guess for values of latent variables in generative model for robot sensory-motor behaviour primitives. We conducted series of experiments where we trained a recurrent neural network to generate sensory-motor sequences for robotic manipulator with 9 degrees of freedom. Experimental results demonstrate substantial improvement in generalisation abilities for unobserved samples in the case of initialization of latent variables with random linear projection of motor data over initialization with zero or random values. Moreover, latent space is well-structured wherein samples belonging to different primitives are well separated from the onset of training process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge