Ensemble Clustering for Graphs: Comparisons and Applications

We recently proposed a new ensemble clustering algorithm for graphs (ECG) based on the concept of consensus clustering. We validated our approach by replicating a study comparing graph clustering algorithms over benchmark graphs, showing that ECG outperforms the leading algorithms. In this paper, we extend our comparison by considering a wider range of parameters for the benchmark, generating graphs with different properties. We provide new experimental results showing that the ECG algorithm alleviates the well-known resolution limit issue, and that it leads to better stability of the partitions. We also illustrate how the ensemble obtained with ECG can be used to quantify the presence of community structure in the graph, and to zoom in on the sub-graph most closely associated with seed vertices. Finally, we illustrate further applications of ECG by comparing it to previous results for community detection on weighted graphs, and community-aware anomaly detection.

Comparing Graph Clusterings: Set partition measures vs. Graph-aware measures

In this paper, we propose a family of graph partition similarity measures that take the topology of the graph into account. These graph-aware measures are alternatives to using set partition similarity measures that are not specifically designed for graph partitions. The two types of measures, graph-aware and set partition measures, are shown to have opposite behaviors with respect to resolution issues and provide complementary information necessary to assess that two graph partitions are similar.

Ensemble Clustering for Graphs

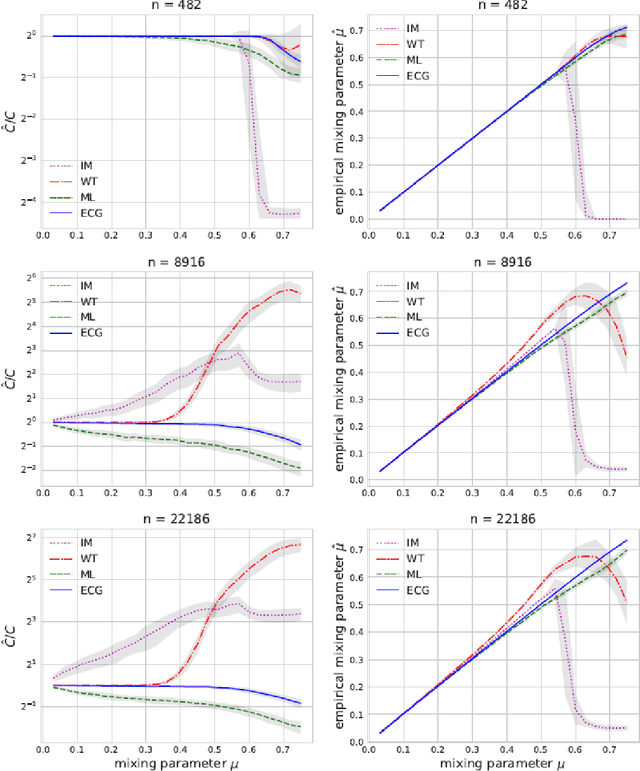
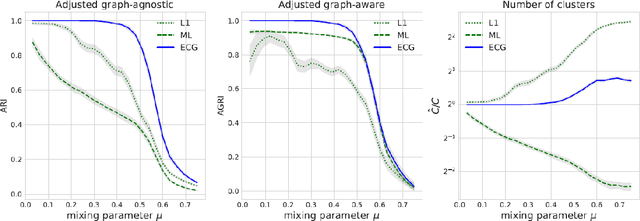
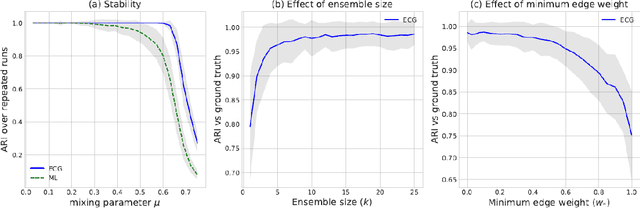
We propose an ensemble clustering algorithm for graphs (ECG), which is based on the Louvain algorithm and the concept of consensus clustering. We validate our approach by replicating a recently published study comparing graph clustering algorithms over artificial networks, showing that ECG outperforms the leading algorithms from that study. We also illustrate how the ensemble obtained with ECG can be used to quantify the presence of community structure in the graph.