Tom Sebastian
An Efficient Approach to Communication-aware Path Planning for Long-range Surveillance Missions undertaken by UAVs
Jul 14, 2017

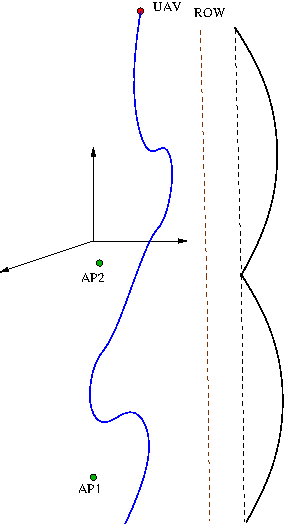
Abstract:While using drones for remote surveillance missions, it is mandatory to do path planning of the vehicle since these are pilot-less vehicles. Path planning, whether offline or online, entails setting up the path as a sequence of locations in the 3D Euclidean space, whose coordinates happen to be latitude, longitude and altitude. For the specific application of remote surveillance of long linear infrastructures in non-urban terrain, the continuous 3D-ESP problem practically entails two important scalar costs. The first scalar cost is the distance traveled along the planned path. Since drones are battery operated, hence it is needed that the path length between fixed start and goal locations of a mission should be minimal at all costs. The other scalar cost is the cost of transmitting the acquired video during the mission of remote surveillance, via a camera mounted in the drone's belly. Because of the length of surveillance target which is long linear infrastructure, the amount of video generated is very high and cannot be generally stored in its entirety, on board. If the connectivity is poor along certain segments of a naive path, to boost video transmission rate, the transmission power of the signal is kept high, which in turn dissipates more battery energy. Hence a path is desired that simultaneously also betters what is known as communication cost. These two costs trade-off, and hence Pareto optimization is needed for this 3D bi-objective Euclidean shortest path problem. In this report, we study the mono-objective offline path planning problem, based on the distance cost, while posing the communication cost as an upper-bounded constraint. The bi-objective path planning solution is sketched out towards the end.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge