Practically Effective Adjustment Variable Selection in Causal Inference

In the estimation of causal effects, one common method for removing the influence of confounders is to adjust the variables that satisfy the back-door criterion. However, it is not always possible to uniquely determine sets of such variables. Moreover, real-world data is almost always limited, which means it may be insufficient for statistical estimation. Therefore, we propose criteria for selecting variables from a list of candidate adjustment variables along with an algorithm to prevent accuracy degradation in causal effect estimation. We initially focus on directed acyclic graphs (DAGs) and then outlines specific steps for applying this method to completed partially directed acyclic graphs (CPDAGs). We also present and prove a theorem on causal effect computation possibility in CPDAGs. Finally, we demonstrate the practical utility of our method using both existing and artificial data.

A Thermodynamical Approach for Probability Estimation

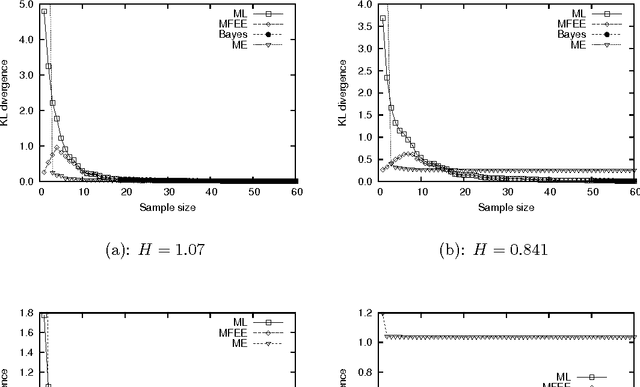
The issue of discrete probability estimation for samples of small size is addressed in this study. The maximum likelihood method often suffers over-fitting when insufficient data is available. Although the Bayesian approach can avoid over-fitting by using prior distributions, it still has problems with objective analysis. In response to these drawbacks, a new theoretical framework based on thermodynamics, where energy and temperature are introduced, was developed. Entropy and likelihood are placed at the center of this method. The key principle of inference for probability mass functions is the minimum free energy, which is shown to unify the two principles of maximum likelihood and maximum entropy. Our method can robustly estimate probability functions from small size data.