Stephon Alexander
The Physics of Machine Learning: An Intuitive Introduction for the Physical Scientist
Nov 27, 2021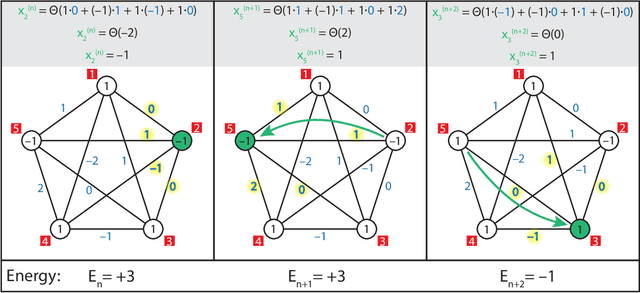

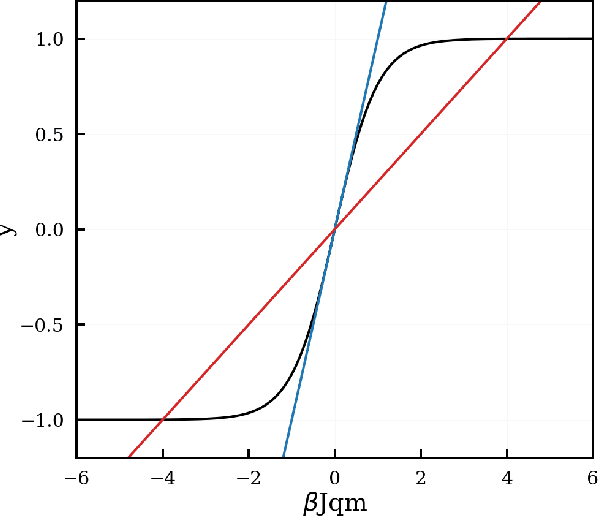
Abstract:This article is intended for physical scientists who wish to gain deeper insights into machine learning algorithms which we present via the domain they know best, physics. We begin with a review of two energy-based machine learning algorithms, Hopfield networks and Boltzmann machines, and their connection to the Ising model. This serves as a foundation to understand the phenomenon of learning more generally. Equipped with this intuition we then delve into additional, more "practical," machine learning architectures including feedforward neural networks, convolutional neural networks, and autoencoders. We also provide code that explicitly demonstrates training a neural network with gradient descent.
The Autodidactic Universe
Mar 29, 2021
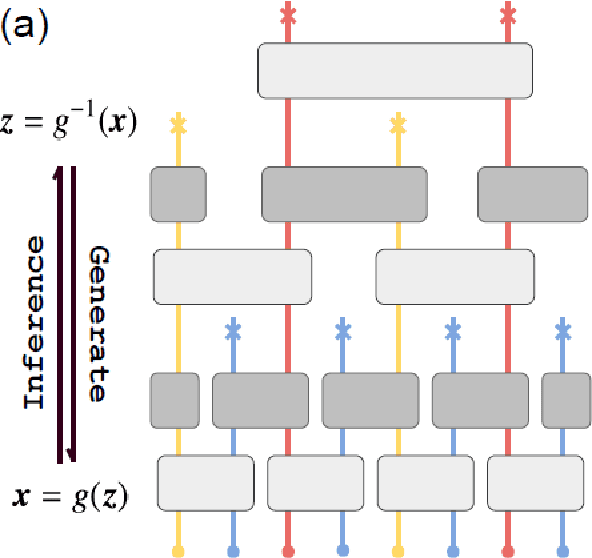

Abstract:We present an approach to cosmology in which the Universe learns its own physical laws. It does so by exploring a landscape of possible laws, which we express as a certain class of matrix models. We discover maps that put each of these matrix models in correspondence with both a gauge/gravity theory and a mathematical model of a learning machine, such as a deep recurrent, cyclic neural network. This establishes a correspondence between each solution of the physical theory and a run of a neural network. This correspondence is not an equivalence, partly because gauge theories emerge from $N \rightarrow \infty $ limits of the matrix models, whereas the same limits of the neural networks used here are not well-defined. We discuss in detail what it means to say that learning takes place in autodidactic systems, where there is no supervision. We propose that if the neural network model can be said to learn without supervision, the same can be said for the corresponding physical theory. We consider other protocols for autodidactic physical systems, such as optimization of graph variety, subset-replication using self-attention and look-ahead, geometrogenesis guided by reinforcement learning, structural learning using renormalization group techniques, and extensions. These protocols together provide a number of directions in which to explore the origin of physical laws based on putting machine learning architectures in correspondence with physical theories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge