Fixed set search applied to the traveling salesman problem

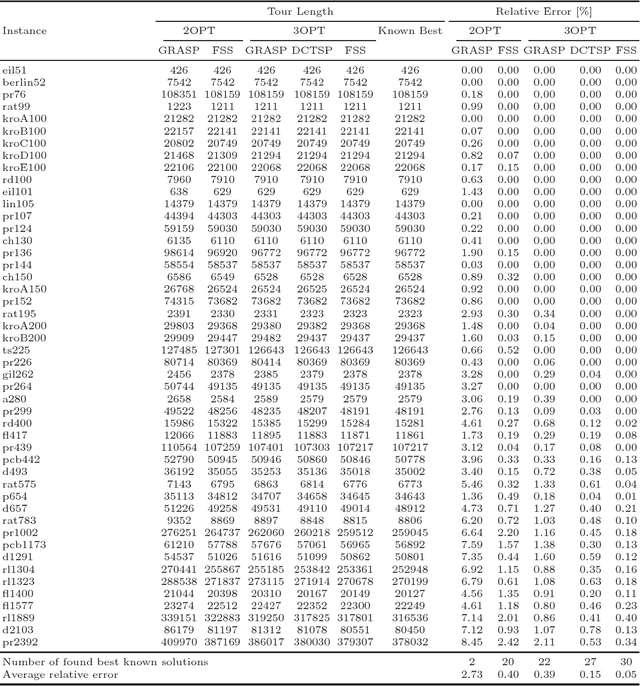
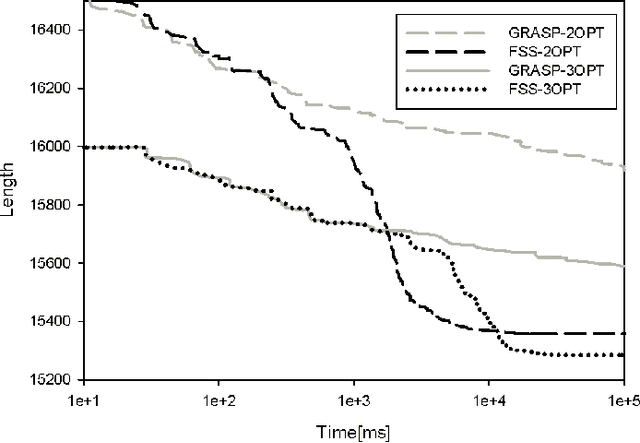
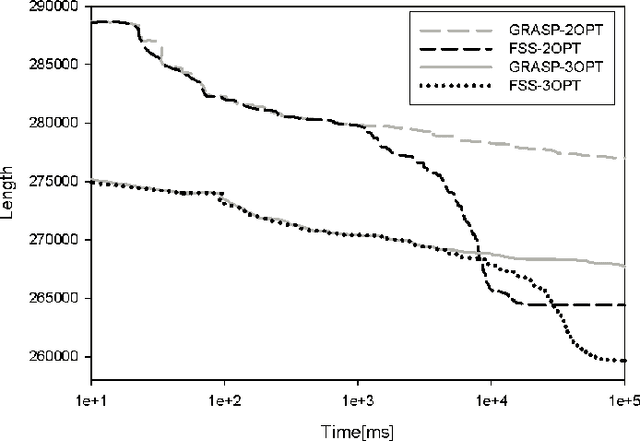
In this paper we present a new population based metaheuristic called the fixed set search (FSS). The proposed approach represents a method of adding a learning mechanism to the greedy randomized adaptive search procedure (GRASP). The basic concept of FSS is to avoid focusing on specific high quality solutions but on parts or elements that such solutions have. This is done through fixing a set of elements that exist in such solutions and dedicating computational effort to finding near optimal solutions for the underlying subproblem. The simplicity of implementing the proposed method is illustrated on the traveling salesman problem. Our computational experiments show that the FSS manages to find significantly better solutions than the GRASP it is based on and also the dynamic convexized method.

An Ant Colony Optimization Algorithm for Partitioning Graphs with Supply and Demand

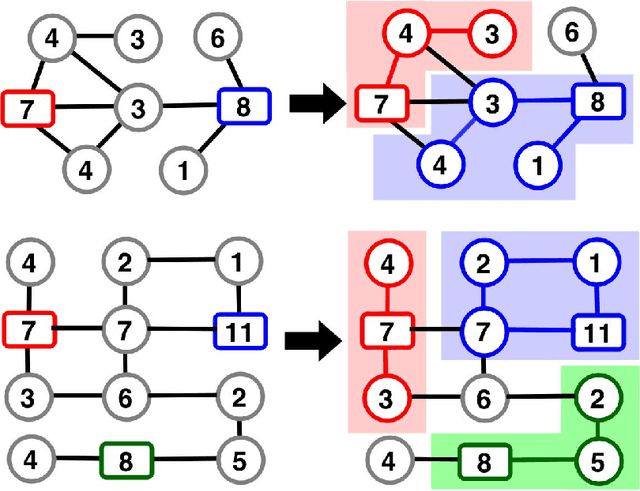
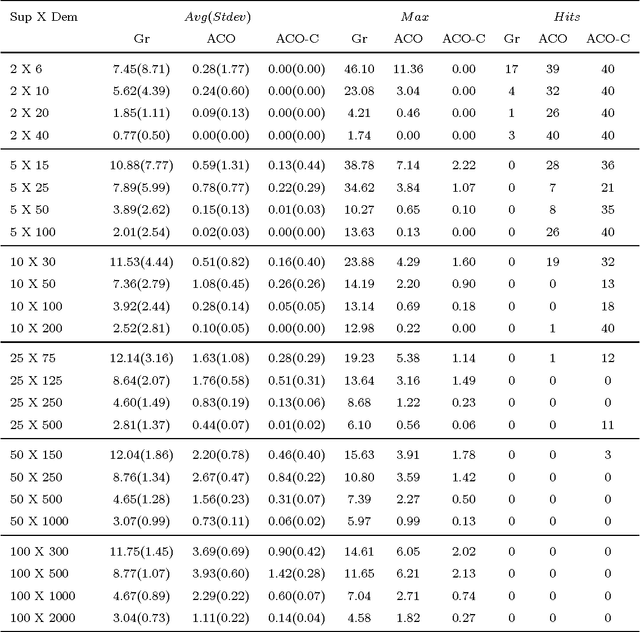
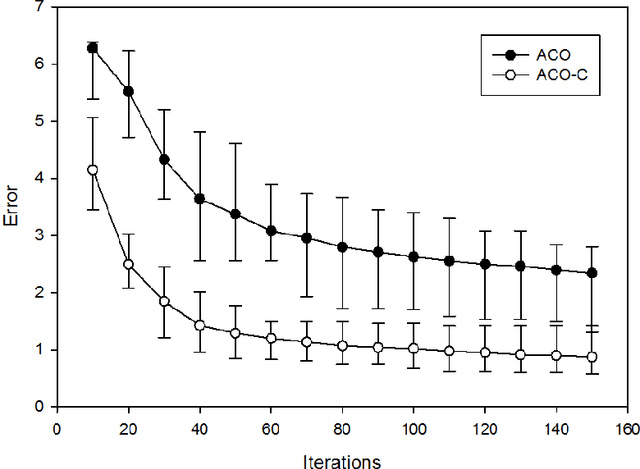
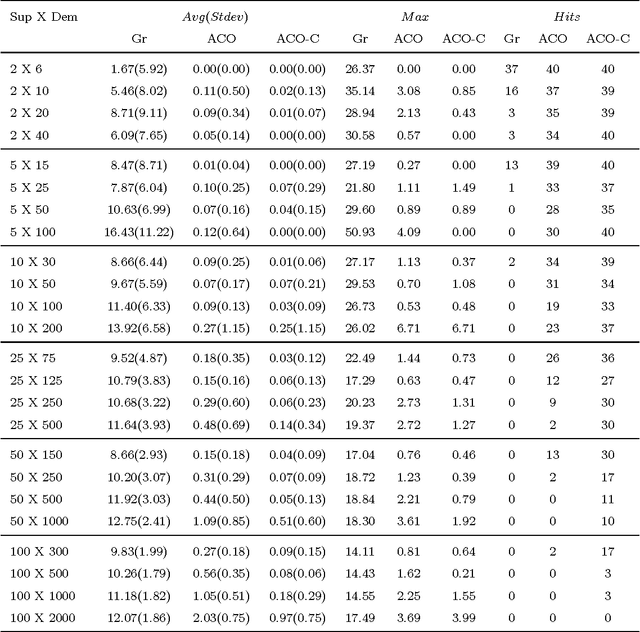
In this paper we focus on finding high quality solutions for the problem of maximum partitioning of graphs with supply and demand (MPGSD). There is a growing interest for the MPGSD due to its close connection to problems appearing in the field of electrical distribution systems, especially for the optimization of self-adequacy of interconnected microgrids. We propose an ant colony optimization algorithm for the problem. With the goal of further improving the algorithm we combine it with a previously developed correction procedure. In our computational experiments we evaluate the performance of the proposed algorithm on both trees and general graphs. The tests show that the method manages to find optimal solutions in more than 50% of the problem instances, and has an average relative error of less than 0.5% when compared to known optimal solutions.

A Heuristic Method for Solving the Problem of Partitioning Graphs with Supply and Demand

In this paper we present a greedy algorithm for solving the problem of the maximum partitioning of graphs with supply and demand (MPGSD). The goal of the method is to solve the MPGSD for large graphs in a reasonable time limit. This is done by using a two stage greedy algorithm, with two corresponding types of heuristics. The solutions acquired in this way are improved by applying a computationally inexpensive, hill climbing like, greedy correction procedure. In our numeric experiments we analyze different heuristic functions for each stage of the greedy algorithm, and show that their performance is highly dependent on the properties of the specific instance. Our tests show that by exploring a relatively small number of solutions generated by combining different heuristic functions, and applying the proposed correction procedure we can find solutions within only a few percent of the optimal ones.

A Multi-Heuristic Approach for Solving the Pre-Marshalling Problem

Minimizing the number of reshuffling operations at maritime container terminals incorporates the Pre-Marshalling Problem (PMP) as an important problem. Based on an analysis of existing solution approaches we develop new heuristics utilizing specific properties of problem instances of the PMP. We show that the heuristic performance is highly dependent on these properties. We introduce a new method that exploits a greedy heuristic of four stages, where for each of these stages several different heuristics may be applied. Instead of using randomization to improve the performance of the heuristic, we repetitively generate a number of solutions by using a combination of different heuristics for each stage. In doing so, only a small number of solutions is generated for which we intend that they do not have undesirable properties, contrary to the case when simple randomization is used. Our experiments show that such a deterministic algorithm significantly outperforms the original nondeterministic method when the quality of found solutions is observed, with a much lower number of generated solutions.

Neigborhood Selection in Variable Neighborhood Search

Variable neighborhood search (VNS) is a metaheuristic for solving optimization problems based on a simple principle: systematic changes of neighborhoods within the search, both in the descent to local minima and in the escape from the valleys which contain them. Designing these neighborhoods and applying them in a meaningful fashion is not an easy task. Moreover, an appropriate order in which they are applied must be determined. In this paper we attempt to investigate this issue. Assume that we are given an optimization problem that is intended to be solved by applying the VNS scheme, how many and which types of neighborhoods should be investigated and what could be appropriate selection criteria to apply these neighborhoods. More specifically, does it pay to "look ahead" (see, e.g., in the context of VNS and GRASP) when attempting to switch from one neighborhood to another?