Sravanthi Gurugubelli
Generative Models and Learning Algorithms for Core-Periphery Structured Graphs
Oct 04, 2022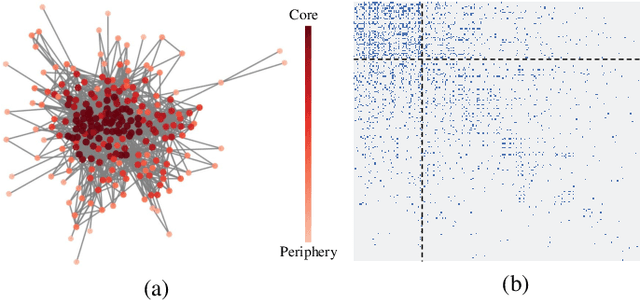
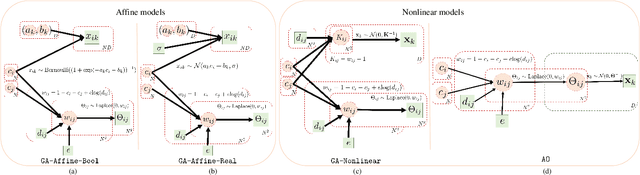
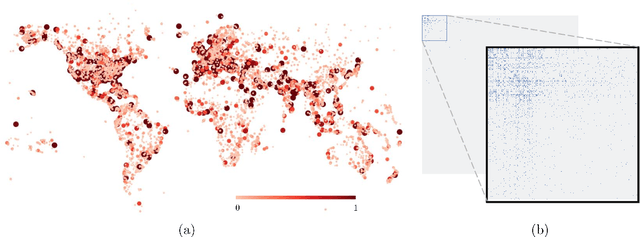
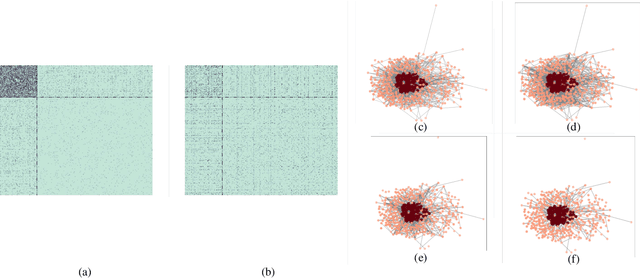
Abstract:We consider core-periphery structured graphs, which are graphs with a group of densely and sparsely connected nodes, respectively, referred to as core and periphery nodes. The so-called core score of a node is related to the likelihood of it being a core node. In this paper, we focus on learning the core scores of a graph from its node attributes and connectivity structure. To this end, we propose two classes of probabilistic graphical models: affine and nonlinear. First, we describe affine generative models to model the dependence of node attributes on its core scores, which determine the graph structure. Next, we discuss nonlinear generative models in which the partial correlations of node attributes influence the graph structure through latent core scores. We develop algorithms for inferring the model parameters and core scores of a graph when both the graph structure and node attributes are available. When only the node attributes of graphs are available, we jointly learn a core-periphery structured graph and its core scores. We provide results from numerical experiments on several synthetic and real-world datasets to demonstrate the efficacy of the developed models and algorithms.
Learning Sparse Graphs with a Core-periphery Structure
Oct 08, 2021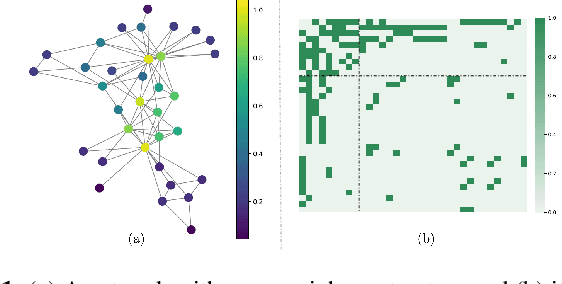
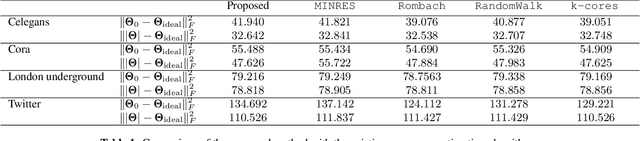
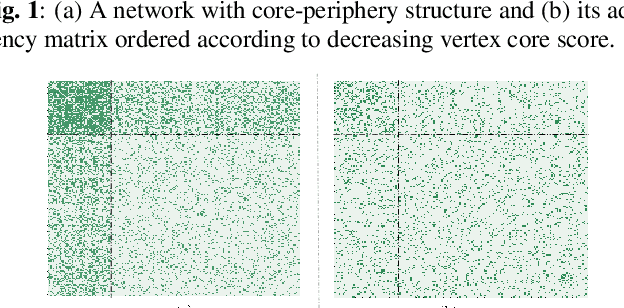

Abstract:In this paper, we focus on learning sparse graphs with a core-periphery structure. We propose a generative model for data associated with core-periphery structured networks to model the dependence of node attributes on core scores of the nodes of a graph through a latent graph structure. Using the proposed model, we jointly infer a sparse graph and nodal core scores that induce dense (sparse) connections in core (respectively, peripheral) parts of the network. Numerical experiments on a variety of real-world data indicate that the proposed method learns a core-periphery structured graph from node attributes alone, while simultaneously learning core score assignments that agree well with existing works that estimate core scores using graph as input and ignoring commonly available node attributes.
Graph Learning for Clustering Multi-view Data
Oct 23, 2020
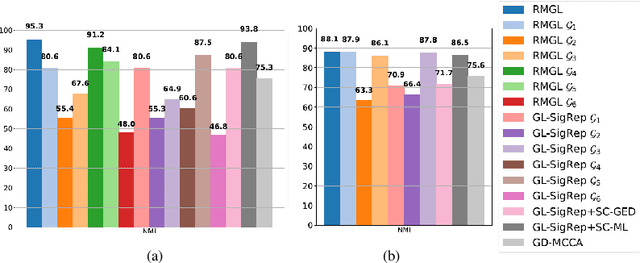
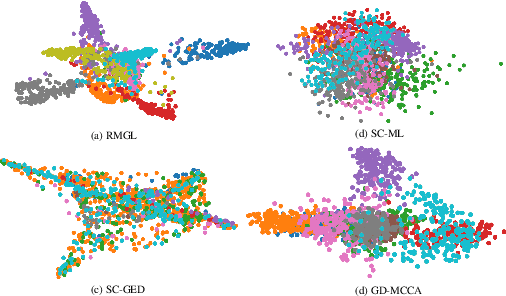
Abstract:In this paper, we focus on graph learning from multi-view data of shared entities for clustering. We can explain interactions between the entities in multi-view data using a multi-layer graph with a common vertex set representing the shared entities. The edges on different layers capture the relationships of the entities. Assuming a smoothness data model, we estimate the graph Laplacian matrices of the individual graph layers by constraining their ranks to obtain multi-component graph layers for clustering. We also learn low-dimensional node embeddings, common to all the views, that assimilate the complementary information present in the views. We propose an efficient solver based on alternating minimization to solve the proposed multi-layer multi-component graph learning problem. Numerical experiments on synthetic and real datasets demonstrate that the proposed algorithm outperforms state-of-the-art multi-view clustering techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge