Extended Koopman Models

We introduce two novel generalizations of the Koopman operator method of nonlinear dynamic modeling. Each of these generalizations leads to greatly improved predictive performance without sacrificing a unique trait of Koopman methods: the potential for fast, globally optimal control of nonlinear, nonconvex systems. The first generalization, Convex Koopman Models, uses convex rather than linear dynamics in the lifted space. The second, Extended Koopman Models, additionally introduces an invertible transformation of the control signal which contributes to the lifted convex dynamics. We describe a deep learning architecture for parameterizing these classes of models, and show experimentally that each significantly outperforms traditional Koopman models in trajectory prediction for two nonlinear, nonconvex dynamic systems.

Coarse-Grained Nonlinear System Identification

We introduce Coarse-Grained Nonlinear Dynamics, an efficient and universal parameterization of nonlinear system dynamics based on the Volterra series expansion. These models require a number of parameters only quasilinear in the system's memory regardless of the order at which the Volterra expansion is truncated; this is a superpolynomial reduction in the number of parameters as the order becomes large. This efficient parameterization is achieved by coarse-graining parts of the system dynamics that depend on the product of temporally distant input samples; this is conceptually similar to the coarse-graining that the fast multipole method uses to achieve $\mathcal{O}(n)$ simulation of n-body dynamics. Our efficient parameterization of nonlinear dynamics can be used for regularization, leading to Coarse-Grained Nonlinear System Identification, a technique which requires very little experimental data to identify accurate nonlinear dynamic models. We demonstrate the properties of this approach on a simple synthetic problem. We also demonstrate this approach experimentally, showing that it identifies an accurate model of the nonlinear voltage to luminosity dynamics of a tungsten filament with less than a second of experimental data.

Neural Group Actions

We introduce an algorithm for designing Neural Group Actions, collections of deep neural network architectures which model symmetric transformations satisfying the laws of a given finite group. This generalizes involutive neural networks $\mathcal{N}$, which satisfy $\mathcal{N}(\mathcal{N}(x))=x$ for any data $x$, the group law of $\mathbb{Z}_2$. We show how to optionally enforce an additional constraint that the group action be volume-preserving. We conjecture, by analogy to a universality result for involutive neural networks, that generative models built from Neural Group Actions are universal approximators for collections of probabilistic transitions adhering to the group laws. We demonstrate experimentally that a Neural Group Action for the quaternion group $Q_8$ can learn how a set of nonuniversal quantum gates satisfying the $Q_8$ group laws act on single qubit quantum states.

Deep Involutive Generative Models for Neural MCMC

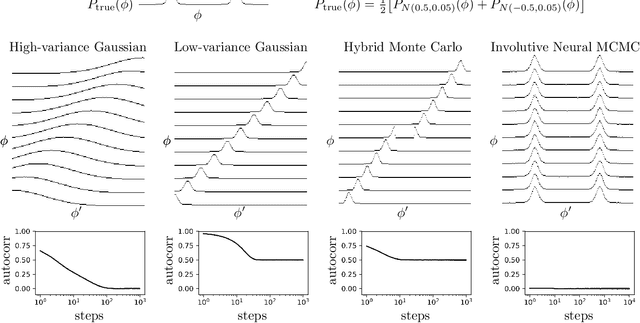
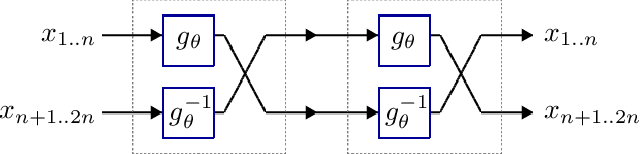
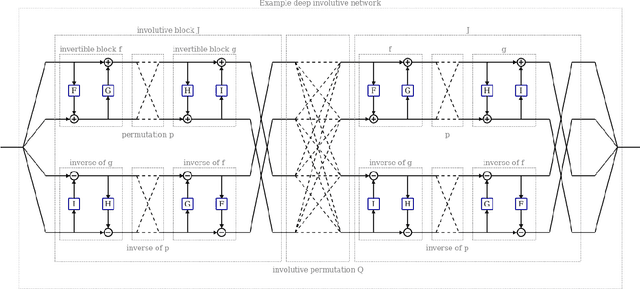
We introduce deep involutive generative models, a new architecture for deep generative modeling, and use them to define Involutive Neural MCMC, a new approach to fast neural MCMC. An involutive generative model represents a probability kernel $G(\phi \mapsto \phi')$ as an involutive (i.e., self-inverting) deterministic function $f(\phi, \pi)$ on an enlarged state space containing auxiliary variables $\pi$. We show how to make these models volume preserving, and how to use deep volume-preserving involutive generative models to make valid Metropolis-Hastings updates based on an auxiliary variable scheme with an easy-to-calculate acceptance ratio. We prove that deep involutive generative models and their volume-preserving special case are universal approximators for probability kernels. This result implies that with enough network capacity and training time, they can be used to learn arbitrarily complex MCMC updates. We define a loss function and optimization algorithm for training parameters given simulated data. We also provide initial experiments showing that Involutive Neural MCMC can efficiently explore multi-modal distributions that are intractable for Hybrid Monte Carlo, and can converge faster than A-NICE-MC, a recently introduced neural MCMC technique.