Sonja Kuhnt
Gaussian Process Models with Low-Rank Correlation Matrices for Both Continuous and Categorical Inputs
Oct 06, 2020
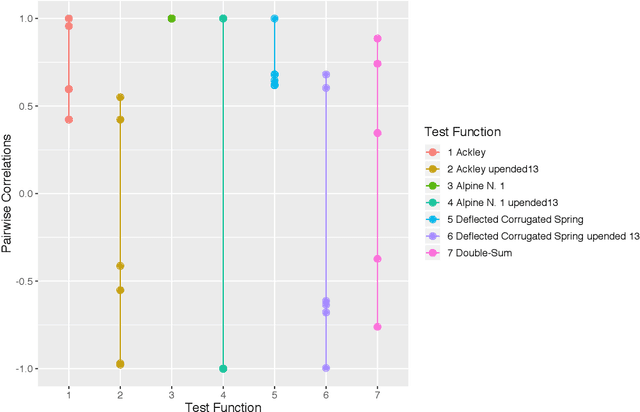
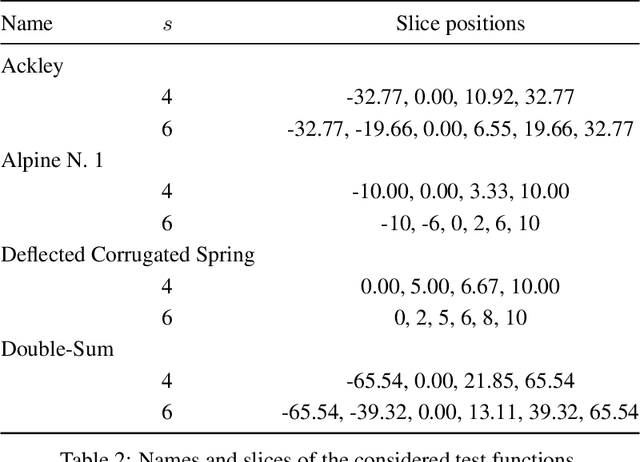
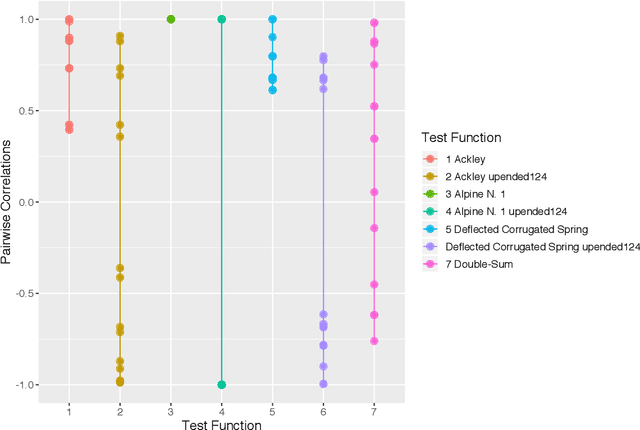
Abstract:We introduce a method that uses low-rank approximations of cross-correlation matrices in mixed continuous and categorical Gaussian Process models. This new method -- called Low-Rank Correlation (LRC) -- offers the ability to flexibly adapt the number of parameters to the problem at hand by choosing an appropriate rank of the approximation. Furthermore, we present a systematic approach of defining test functions that can be used for assessing the accuracy of models or optimization methods that are concerned with both continuous and categorical inputs. We compare LRC to existing approaches of modeling the cross-correlation matrix. It turns out that the new approach performs well in terms of estimation of cross-correlations and response surface prediction. Therefore, LRC is a flexible and useful addition to existing methods, especially for increasing numbers of combinations of levels of the categorical inputs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge