QonFusion -- Quantum Approaches to Gaussian Random Variables: Applications in Stable Diffusion and Brownian Motion

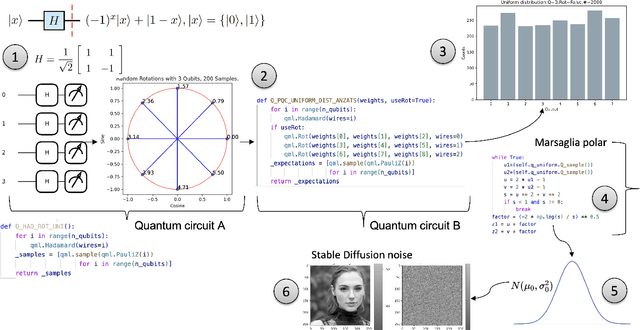
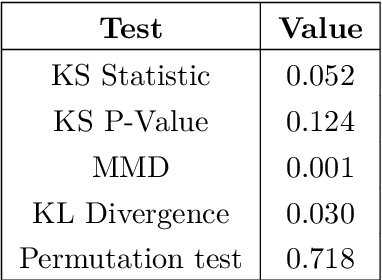
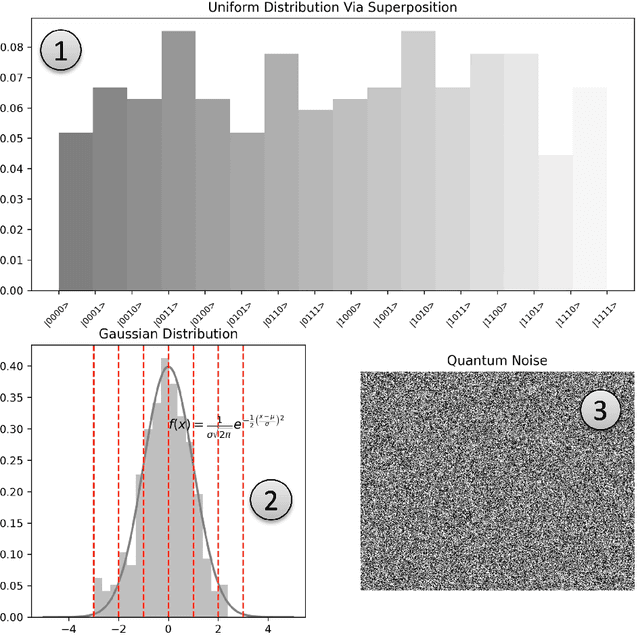
In the present study, we delineate a strategy focused on non-parametric quantum circuits for the generation of Gaussian random variables (GRVs). This quantum-centric approach serves as a substitute for conventional pseudorandom number generators (PRNGs), such as the \textbf{torch.rand} function in PyTorch. The principal theme of our research is the incorporation of Quantum Random Number Generators (QRNGs) into classical models of diffusion. Notably, our Quantum Gaussian Random Variable Generator fulfills dual roles, facilitating simulations in both Stable Diffusion (SD) and Brownian Motion (BM). This diverges markedly from prevailing methods that utilize parametric quantum circuits (PQCs), often in conjunction with variational quantum eigensolvers (VQEs). Although conventional techniques can accurately approximate ground states in complex systems or model elaborate probability distributions, they require a computationally demanding optimization process to tune parameters. Our non-parametric strategy obviates this necessity. To facilitate assimilating our methodology into existing computational frameworks, we put forward QonFusion, a Python library congruent with both PyTorch and PennyLane, functioning as a bridge between classical and quantum computational paradigms. We validate QonFusion through extensive statistical testing, including tests which confirm the statistical equivalence of the Gaussian samples from our quantum approach to classical counterparts within defined significance limits. QonFusion is available at \url{https://boltzmannentropy.github.io/qonfusion.github.io/} to reproduce all findings here.

A quantum Fourier transform (QFT) based note detection algorithm

In quantum information processing (QIP), the quantum Fourier transform (QFT) has a plethora of applications [1] [2] [3]: Shor's algorithm and phase estimation are just a few well-known examples. Shor's quantum factorization algorithm, one of the most widely quoted quantum algorithms [4] [5] [6] relies heavily on the QFT and efficiently finds integer prime factors of large numbers on quantum computers [4]. This seminal ground-breaking design for quantum algorithms has triggered a cascade of viable alternatives to previously unsolvable problems on a classical computer that are potentially superior and can run in polynomial time. In this work we examine the QFT's structure and implementation for the creation of a quantum music note detection algorithm both on a simulated and a real quantum computer. Though formal approaches [7] [1] [8] [9] exist for the verification of quantum algorithms, in this study we limit ourselves to a simpler, symbolic representation which we validate using the symbolic SymPy [10] [11] package which symbolically replicates quantum computing processes. The algorithm is then implemented as a quantum circuit, using IBM's qiskit [12] library and finally period detection is exemplified on an actual single musical tone using a varying number of qubits.

Deep Learning Interviews: Hundreds of fully solved job interview questions from a wide range of key topics in AI

The second edition of Deep Learning Interviews is home to hundreds of fully-solved problems, from a wide range of key topics in AI. It is designed to both rehearse interview or exam specific topics and provide machine learning MSc / PhD. students, and those awaiting an interview a well-organized overview of the field. The problems it poses are tough enough to cut your teeth on and to dramatically improve your skills-but they're framed within thought-provoking questions and engaging stories. That is what makes the volume so specifically valuable to students and job seekers: it provides them with the ability to speak confidently and quickly on any relevant topic, to answer technical questions clearly and correctly, and to fully understand the purpose and meaning of interview questions and answers. Those are powerful, indispensable advantages to have when walking into the interview room. The book's contents is a large inventory of numerous topics relevant to DL job interviews and graduate level exams. That places this work at the forefront of the growing trend in science to teach a core set of practical mathematical and computational skills. It is widely accepted that the training of every computer scientist must include the fundamental theorems of ML, and AI appears in the curriculum of nearly every university. This volume is designed as an excellent reference for graduates of such programs.