Shigenobu Kobayashi
Theoretical foundation for CMA-ES from information geometric perspective
Jun 04, 2012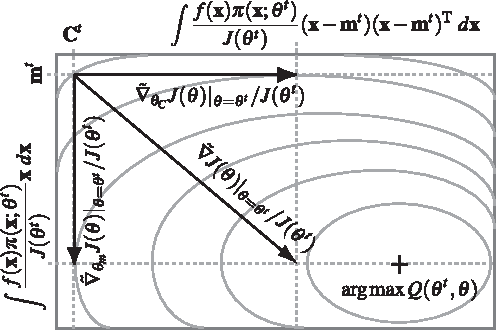
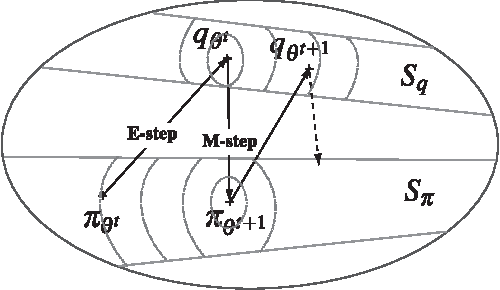
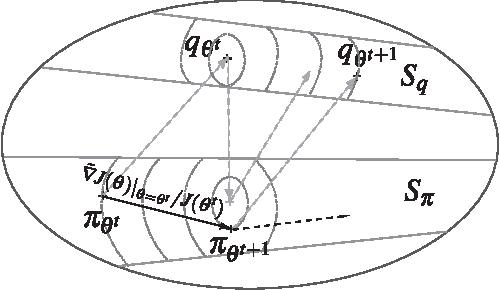
Abstract:This paper explores the theoretical basis of the covariance matrix adaptation evolution strategy (CMA-ES) from the information geometry viewpoint. To establish a theoretical foundation for the CMA-ES, we focus on a geometric structure of a Riemannian manifold of probability distributions equipped with the Fisher metric. We define a function on the manifold which is the expectation of fitness over the sampling distribution, and regard the goal of update of the parameters of sampling distribution in the CMA-ES as maximization of the expected fitness. We investigate the steepest ascent learning for the expected fitness maximization, where the steepest ascent direction is given by the natural gradient, which is the product of the inverse of the Fisher information matrix and the conventional gradient of the function. Our first result is that we can obtain under some types of parameterization of multivariate normal distribution the natural gradient of the expected fitness without the need for inversion of the Fisher information matrix. We find that the update of the distribution parameters in the CMA-ES is the same as natural gradient learning for expected fitness maximization. Our second result is that we derive the range of learning rates such that a step in the direction of the exact natural gradient improves the parameters in the expected fitness. We see from the close relation between the CMA-ES and natural gradient learning that the default setting of learning rates in the CMA-ES seems suitable in terms of monotone improvement in expected fitness. Then, we discuss the relation to the expectation-maximization framework and provide an information geometric interpretation of the CMA-ES.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge