Shawn C. Eastwood
Information Fusion on Belief Networks
Jul 25, 2020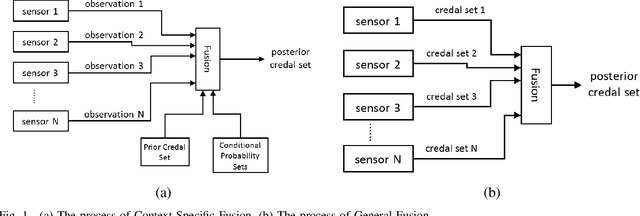

Abstract:This paper will focus on the process of 'fusing' several observations or models of uncertainty into a single resultant model. Many existing approaches to fusion use subjective quantities such as 'strengths of belief' and process these quantities with heuristic algorithms. This paper argues in favor of quantities that can be objectively measured, as opposed to the subjective 'strength of belief' values. This paper will focus on probability distributions, and more importantly, structures that denote sets of probability distributions known as 'credal sets'. The novel aspect of this paper will be a taxonomy of models of fusion that use specific types of credal sets, namely probability interval distributions and Dempster-Shafer models. An objective requirement for information fusion algorithms is provided, and is satisfied by all models of fusion presented in this paper. Dempster's rule of combination is shown to not satisfy this requirement. This paper will also assess the computational challenges involved for the proposed fusion approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge