Muscle-inspired flexible mechanical logic architecture for colloidal robotics

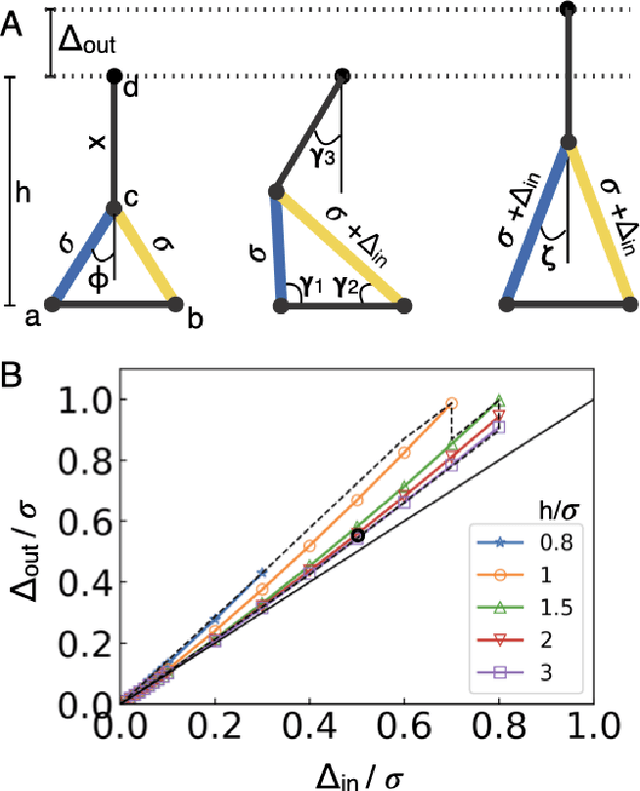
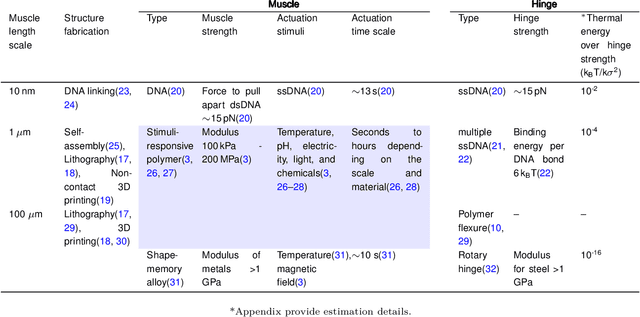
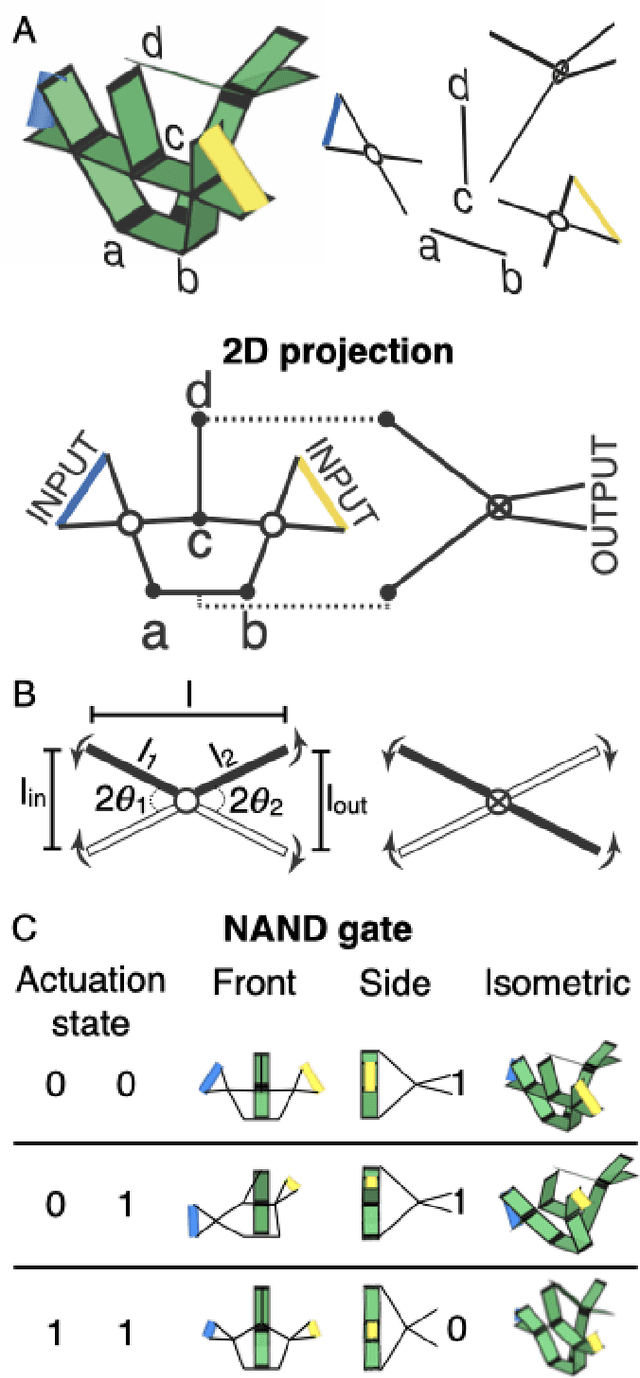
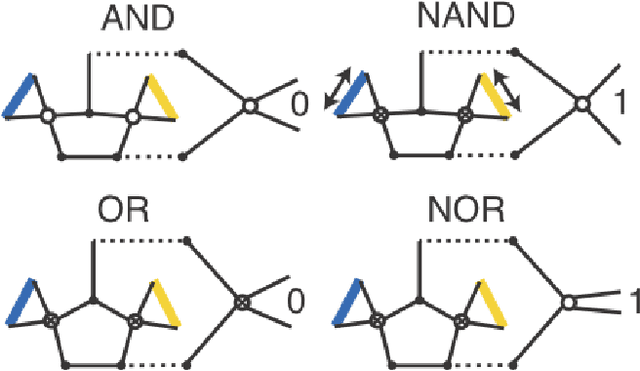
Materials that respond to external stimuli by expanding or contracting provide a transduction route that integrates sensing and actuation powered directly by the stimuli. This motivates us to build colloidal scale robots using these materials that can morph into arbitrary configurations. For intelligent use of global stimuli in robotic systems, computation ability needs to be incorporated within them. The challenge is to design an architecture that is compact, material agnostic, stable under stochastic forces and can employ stimuli-responsive materials. We present an architecture that computes combinatorial logic using mechanical gates that use muscle-like response - expansion and contraction - as circuit signal with additional benefits of logic circuitry being physically flexible and able to be retrofit to arbitrary robot bodies. We mathematically analyze gate geometry and discuss tuning it for the given requirements of signal dimension and magnitude. We validate the function and stability of the design at the colloidal scale using Brownian dynamics simulations. We also demonstrate the gate design using a 3D printed model. Finally, we simulate a complete robot that folds into Tetris shapes.

Harmonic Order Parameters for Characterizing Complex Particle Morphologies

Order parameters based on spherical harmonics and Fourier coefficients already play a significant role in condensed matter research in the context of systems of spherical or point particles. Here, we extend these types of order parameter to more complex shapes, such as those encountered in nanoscale self-assembly applications. To do so, we build on a powerful set of techniques that originate in the computer science field of "shape matching." We demonstrate how shape matching techniques can be applied to identify unknown structures and create highly-specialized \textit{ad hoc} order parameters. Additionally, we investigate the special symmetry properties of harmonic descriptors, and demonstrate how they can be exploited to provide optimal solutions to certain classes of problems. Our techniques can be applied to particle systems in general, both simulated and experimental, provided the particle positions are known.

Characterizing Structure Through Shape Matching and Applications to Self Assembly

Structural quantities such as order parameters and correlation functions are often employed to gain insight into the physical behavior and properties of condensed matter systems. While standard quantities for characterizing structure exist, often they are insufficient for treating problems in the emerging field of nano and microscale self-assembly, where the structures encountered may be complex and unusual. The computer science field of "shape matching" offers a robust solution to this problem by defining diverse methods for quantifying the similarity between arbitrarily complex shapes. Most order parameters and correlation functions used in condensed matter apply a specific measure of structural similarity within the context of a broader scheme. By substituting shape matching quantities for traditional quantities, we retain the essence of the broader scheme, but extend its applicability to more complex structures. Here we review some standard shape matching techniques and discuss how they might be used to create highly flexible structural metrics for diverse systems such as self-assembled matter. We provide three proof-of-concept example problems applying shape matching methods to identifying local and global structures, and tracking structural transitions in complex assembled systems. The shape matching methods reviewed here are applicable to a wide range of condensed matter systems, both simulated and experimental, provided particle positions are known or can be accurately imaged.