Machine learning-guided construction of an analytic kinetic energy functional for orbital free density functional theory

Machine learning (ML) of kinetic energy functionals (KEF) for orbital-free density functional theory (OF-DFT) holds the promise of addressing an important bottleneck in large-scale ab initio materials modeling where sufficiently accurate analytic KEFs are lacking. However, ML models are not as easily handled as analytic expressions; they need to be provided in the form of algorithms and associated data. Here, we bridge the two approaches and construct an analytic expression for a KEF guided by interpretative machine learning of crystal cell-averaged kinetic energy densities ({\tau}) of several hundred materials. A previously published dataset including multiple phases of 433 unary, binary, and ternary compounds containing Li, Al, Mg, Si, As, Ga, Sb, Na, Sn, P, and In was used for training, including data at the equilibrium geometry as well as strained structures. A hybrid Gaussian process regression - neural network (GPR-NN) method was used to understand the type of functional dependence of {\tau} on the features which contained cell-averaged terms of the 4th order gradient expansion and the product of the electron density and Kohn-Sham effective potential. Based on this analysis, an analytic model is constructed that can reproduce Kohn-Sham DFT energy-volume curves with sufficient accuracy (pronounced minima that are sufficiently close to the minima of the Kohn-Sham DFT-based curves and with sufficiently close curvatures) to enable structure optimizations and elastic response calculations.

Degeneration of kernel regression with Matern kernels into low-order polynomial regression in high dimension

Kernel methods such as kernel ridge regression and Gaussian process regressions with Matern type kernels have been increasingly used, in particular, to fit potential energy surfaces (PES) and density functionals, and for materials informatics. When the dimensionality of the feature space is high, these methods are used with necessarily sparse data. In this regime, the optimal length parameter of a Matern-type kernel tends to become so large that the method effectively degenerates into a low-order polynomial regression and therefore loses any advantage over such regression. This is demonstrated theoretically as well as numerically on the examples of six- and fifteen-dimensional molecular PES using squared exponential and simple exponential kernels. The results shed additional light on the success of polynomial approximations such as PIP for medium size molecules and on the importance of orders-of-coupling based models for preserving the advantages of kernel methods with Matern type kernels or on the use of physically-motivated (reproducing) kernels.

Orders-of-coupling representation with a single neural network with optimal neuron activation functions and without nonlinear parameter optimization

Representations of multivariate functions with low-dimensional functions that depend on subsets of original coordinates (corresponding of different orders of coupling) are useful in quantum dynamics and other applications, especially where integration is needed. Such representations can be conveniently built with machine learning methods, and previously, methods building the lower-dimensional terms of such representations with neural networks [e.g. Comput. Phys. Comm. 180 (2009) 2002] and Gaussian process regressions [e.g. Mach. Learn. Sci. Technol. 3 (2022) 01LT02] were proposed. Here, we show that neural network models of orders-of-coupling representations can be easily built by using a recently proposed neural network with optimal neuron activation functions computed with a first-order additive Gaussian process regression [arXiv:2301.05567] and avoiding non-linear parameter optimization. Examples are given of representations of molecular potential energy surfaces.

Neural network with optimal neuron activation functions based on additive Gaussian process regression

Feed-forward neural networks (NN) are a staple machine learning method widely used in many areas of science and technology. While even a single-hidden layer NN is a universal approximator, its expressive power is limited by the use of simple neuron activation functions (such as sigmoid functions) that are typically the same for all neurons. More flexible neuron activation functions would allow using fewer neurons and layers and thereby save computational cost and improve expressive power. We show that additive Gaussian process regression (GPR) can be used to construct optimal neuron activation functions that are individual to each neuron. An approach is also introduced that avoids non-linear fitting of neural network parameters. The resulting method combines the advantage of robustness of a linear regression with the higher expressive power of a NN. We demonstrate the approach by fitting the potential energy surfaces of the water molecule and formaldehyde. Without requiring any non-linear optimization, the additive GPR based approach outperforms a conventional NN in the high accuracy regime, where a conventional NN suffers more from overfitting.

The loss of the property of locality of the kernel in high-dimensional Gaussian process regression on the example of the fitting of molecular potential energy surfaces

Kernel based methods including Gaussian process regression (GPR) and generally kernel ridge regression (KRR) have been finding increasing use in computational chemistry, including the fitting of potential energy surfaces and density functionals in high-dimensional feature spaces. Kernels of the Matern family such as Gaussian-like kernels (basis functions) are often used, which allows imparting them the meaning of covariance functions and formulating GPR as an estimator of the mean of a Gaussian distribution. The notion of locality of the kernel is critical for this interpretation. It is also critical to the formulation of multi-zeta type basis functions widely used in computational chemistry We show, on the example of fitting of molecular potential energy surfaces of increasing dimensionality, the practical disappearance of the property of locality of a Gaussian-like kernel in high dimensionality. We also formulate a multi-zeta approach to the kernel and show that it significantly improves the quality of regression in low dimensionality but loses any advantage in high dimensionality, which is attributed to the loss of the property of locality.

Random Sampling High Dimensional Model Representation Gaussian Process Regression (RS-HDMR-GPR): a Python module for representing multidimensional functions with machine-learned lower-dimensional terms

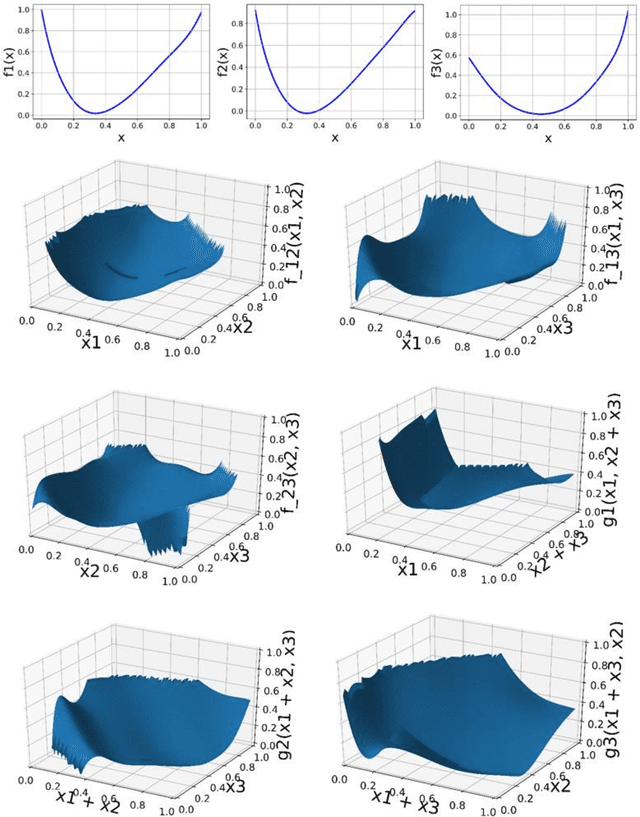
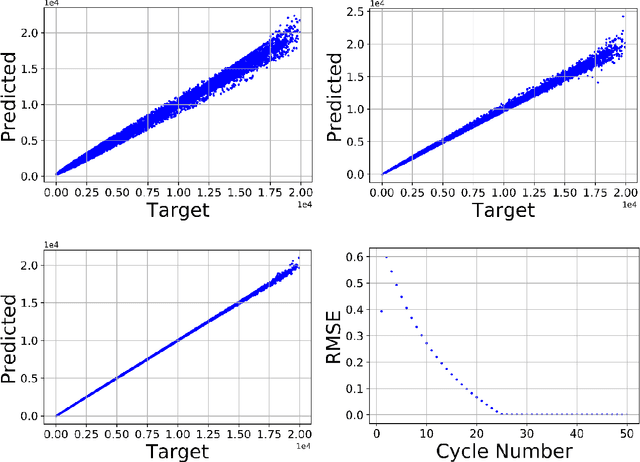
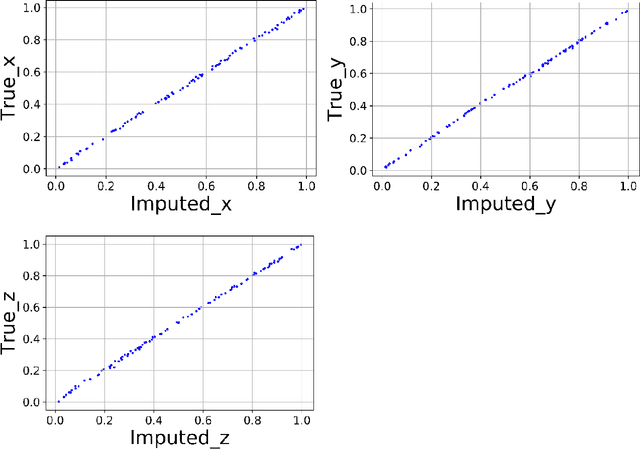
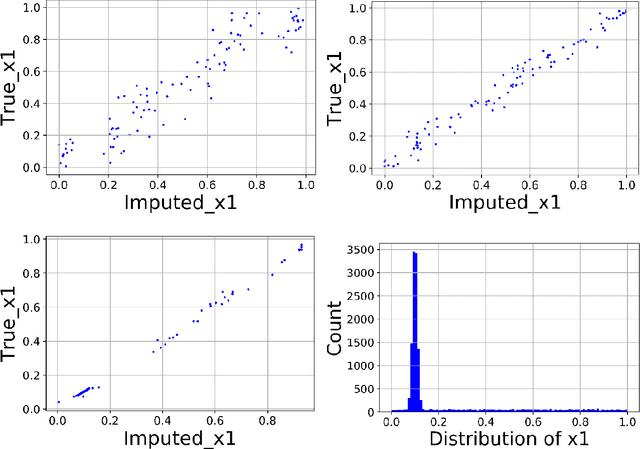
We present a Python implementation for RS-HDMR-GPR (Random Sampling High Dimensional Model Representation Gaussian Process Regression). The method builds representations of multivariate functions with lower-dimensional terms, either as an expansion over orders of coupling or using terms of only a given dimensionality. This facilitates, in particular, recovering functional dependence from sparse data. The code also allows imputation of missing values of the variables. The capabilities of this regression tool are demonstrated on test cases involving synthetic analytic functions, the potential energy surface of the water molecule, and financial market data.