Gaussian Process Manifold Interpolation for Probabilistic Atrial Activation Maps and Uncertain Conduction Velocity

In patients with atrial fibrillation, local activation time (LAT) maps are routinely used for characterising patient pathophysiology. The gradient of LAT maps can be used to calculate conduction velocity (CV), which directly relates to material conductivity and may provide an important measure of atrial substrate properties. Including uncertainty in CV calculations would help with interpreting the reliability of these measurements. Here, we build upon a recent insight into reduced-rank Gaussian processes (GP) to perform probabilistic interpolation of uncertain LAT directly on human atrial manifolds. Our Gaussian Process Manifold Interpolation (GPMI) method accounts for the topology of the atria, and allows for calculation of statistics for predicted CV. We demonstrate our method on two clinical cases, and perform validation against a simulated ground truth. CV uncertainty depends on data density, wave propagation direction, and CV magnitude. GPMI is suitable for probabilistic interpolation of other uncertain quantities on non-Euclidean manifolds.

Accelerating ABC methods using Gaussian processes

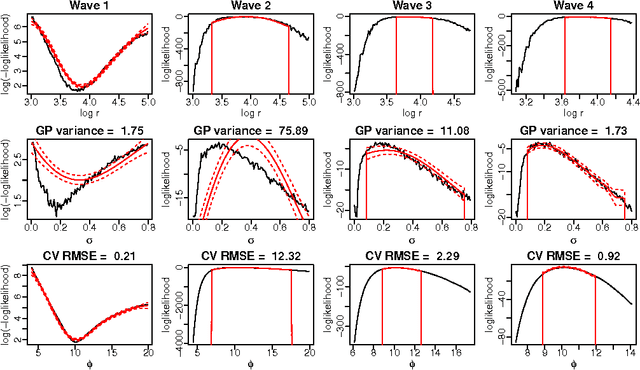
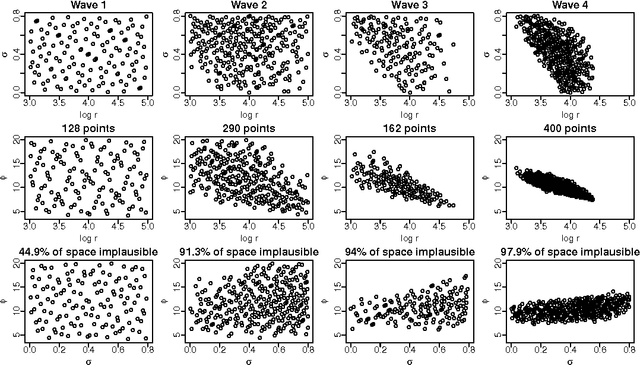
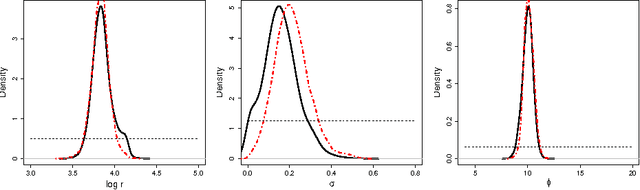
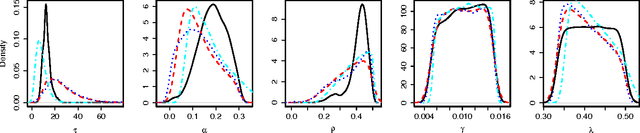
Approximate Bayesian computation (ABC) methods are used to approximate posterior distributions using simulation rather than likelihood calculations. We introduce Gaussian process (GP) accelerated ABC, which we show can significantly reduce the number of simulations required. As computational resource is usually the main determinant of accuracy in ABC, GP-accelerated methods can thus enable more accurate inference in some models. GP models of the unknown log-likelihood function are used to exploit continuity and smoothness, reducing the required computation. We use a sequence of models that increase in accuracy, using intermediate models to rule out regions of the parameter space as implausible. The methods will not be suitable for all problems, but when they can be used, can result in significant computational savings. For the Ricker model, we are able to achieve accurate approximations to the posterior distribution using a factor of 100 fewer simulator evaluations than comparable Monte Carlo approaches, and for a population genetics model we are able to approximate the exact posterior for the first time.