Cellular, Cell-less, and Everything in Between: A Unified Framework for Utility Region Analysis in Wireless Networks

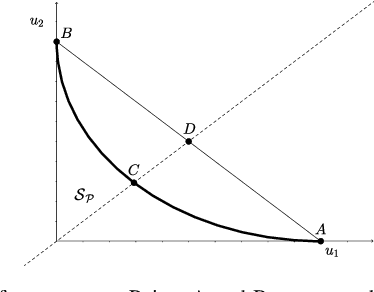
We introduce a unified framework for analyzing utility regions of wireless networks, with a focus on the signal-to-interference-noise-ratio (SINR) and achievable rate regions. The framework provides valuable insights into interference patterns of modern network architectures, such as cell-less and extremely large MIMO networks, and it generalizes existing characterizations of the weak Pareto boundary. A central contribution is the derivation of sufficient conditions that guarantee convexity of the utility regions. Convexity is an important property because it ensures that time sharing (or user grouping) cannot simultaneously increase the utility of all users when the network operates on the weak Pareto boundary. These sufficient conditions also have two key implications. First, they identify a family of (weighted) sum-rate maximization problems that are inherently convex without any variable transformations, thus paving the way for the development of efficient, provably optimal solvers for this family. Second, they provide a rigorous justification for formulating sum-rate maximization problems directly in terms of achievable rates, rather than SINR levels. Our theoretical insights also motivate an alternative to the concept of favorable propagation in the massive MIMO literature -- one that explicitly accounts for self-interference and the beamforming strategy.

Characterization of the weak Pareto boundary of resource allocation problems in wireless networks -- Implications to cell-less systems

We establish necessary and sufficient conditions for a network configuration to provide utilities that are both fair and efficient in a well-defined sense. To cover as many applications as possible with a unified framework, we consider utilities defined in an axiomatic way, and the constraints imposed on the feasible network configurations are expressed with a single inequality involving a monotone norm. In this setting, we prove that a necessary and sufficient condition to obtain network configurations that are efficient in the weak Pareto sense is to select configurations attaining equality in the monotone norm constraint. Furthermore, for a given configuration satisfying this equality, we characterize a criterion for which the configuration can be considered fair for the active links. We illustrate potential implications of the theoretical findings by presenting, for the first time, a simple parametrization based on power vectors of achievable rate regions in modern cell-less systems subject to practical impairments.

Joint optimal beamforming and power control in cell-free massive MIMO

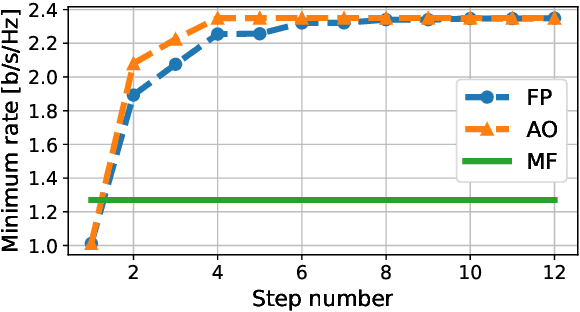
We derive a fast and optimal algorithm for solving practical weighted max-min SINR problems in cell-free massive MIMO networks. For the first time, the optimization problem jointly covers long-term power control and distributed beamforming design under imperfect cooperation. In particular, we consider user-centric clusters of access points cooperating on the basis of possibly limited channel state information sharing. Our optimal algorithm merges powerful power control tools based on interference calculus with the recently developed team theoretic framework for distributed beamforming design. In addition, we propose a variation that shows faster convergence in practice.