VWAP Execution with Signature-Enhanced Transformers: A Multi-Asset Learning Approach

In this paper I propose a novel approach to Volume Weighted Average Price (VWAP) execution that addresses two key practical challenges: the need for asset-specific model training and the capture of complex temporal dependencies. Building upon my recent work in dynamic VWAP execution arXiv:2502.18177, I demonstrate that a single neural network trained across multiple assets can achieve performance comparable to or better than traditional asset-specific models. The proposed architecture combines a transformer-based design inspired by arXiv:2406.02486 with path signatures for capturing geometric features of price-volume trajectories, as in arXiv:2406.17890. The empirical analysis, conducted on hourly cryptocurrency trading data from 80 trading pairs, shows that the globally-fitted model with signature features (GFT-Sig) achieves superior performance in both absolute and quadratic VWAP loss metrics compared to asset-specific approaches. Notably, these improvements persist for out-of-sample assets, demonstrating the model's ability to generalize across different market conditions. The results suggest that combining global parameter sharing with signature-based feature extraction provides a scalable and robust approach to VWAP execution, offering significant practical advantages over traditional asset-specific implementations.

Recurrent Neural Networks for Dynamic VWAP Execution: Adaptive Trading Strategies with Temporal Kolmogorov-Arnold Networks

The execution of Volume Weighted Average Price (VWAP) orders remains a critical challenge in modern financial markets, particularly as trading volumes and market complexity continue to increase. In my previous work arXiv:2502.13722, I introduced a novel deep learning approach that demonstrated significant improvements over traditional VWAP execution methods by directly optimizing the execution problem rather than relying on volume curve predictions. However, that model was static because it employed the fully linear approach described in arXiv:2410.21448, which is not designed for dynamic adjustment. This paper extends that foundation by developing a dynamic neural VWAP framework that adapts to evolving market conditions in real time. We introduce two key innovations: first, the integration of recurrent neural networks to capture complex temporal dependencies in market dynamics, and second, a sophisticated dynamic adjustment mechanism that continuously optimizes execution decisions based on market feedback. The empirical analysis, conducted across five major cryptocurrency markets, demonstrates that this dynamic approach achieves substantial improvements over both traditional methods and our previous static implementation, with execution performance gains of 10 to 15% in liquid markets and consistent outperformance across varying conditions. These results suggest that adaptive neural architectures can effectively address the challenges of modern VWAP execution while maintaining computational efficiency suitable for practical deployment.

Deep Learning for VWAP Execution in Crypto Markets: Beyond the Volume Curve

Volume-Weighted Average Price (VWAP) is arguably the most prevalent benchmark for trade execution as it provides an unbiased standard for comparing performance across market participants. However, achieving VWAP is inherently challenging due to its dependence on two dynamic factors, volumes and prices. Traditional approaches typically focus on forecasting the market's volume curve, an assumption that may hold true under steady conditions but becomes suboptimal in more volatile environments or markets such as cryptocurrency where prediction error margins are higher. In this study, I propose a deep learning framework that directly optimizes the VWAP execution objective by bypassing the intermediate step of volume curve prediction. Leveraging automatic differentiation and custom loss functions, my method calibrates order allocation to minimize VWAP slippage, thereby fully addressing the complexities of the execution problem. My results demonstrate that this direct optimization approach consistently achieves lower VWAP slippage compared to conventional methods, even when utilizing a naive linear model presented in arXiv:2410.21448. They validate the observation that strategies optimized for VWAP performance tend to diverge from accurate volume curve predictions and thus underscore the advantage of directly modeling the execution objective. This research contributes a more efficient and robust framework for VWAP execution in volatile markets, illustrating the potential of deep learning in complex financial systems where direct objective optimization is crucial. Although my empirical analysis focuses on cryptocurrency markets, the underlying principles of the framework are readily applicable to other asset classes such as equities.

STAN: Smooth Transition Autoregressive Networks

Traditional Smooth Transition Autoregressive (STAR) models offer an effective way to model these dynamics through smooth regime changes based on specific transition variables. In this paper, we propose a novel approach by drawing an analogy between STAR models and a multilayer neural network architecture. Our proposed neural network architecture mimics the STAR framework, employing multiple layers to simulate the smooth transition between regimes and capturing complex, nonlinear relationships. The network's hidden layers and activation functions are structured to replicate the gradual switching behavior typical of STAR models, allowing for a more flexible and scalable approach to regime-dependent modeling. This research suggests that neural networks can provide a powerful alternative to STAR models, with the potential to enhance predictive accuracy in economic and financial forecasting.

CaAdam: Improving Adam optimizer using connection aware methods

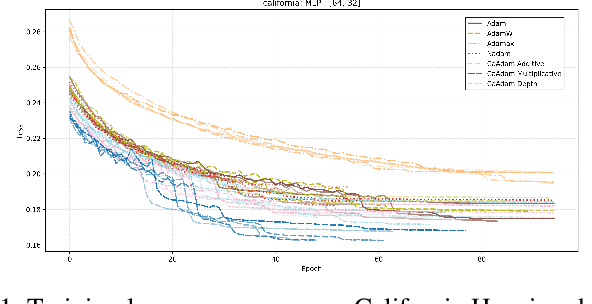
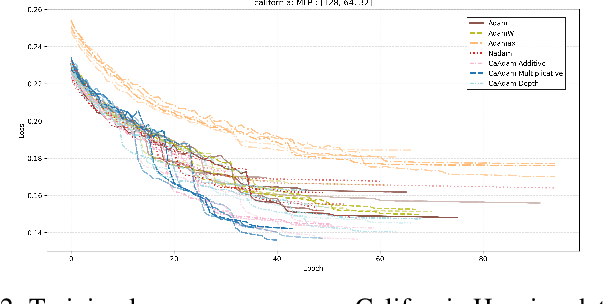
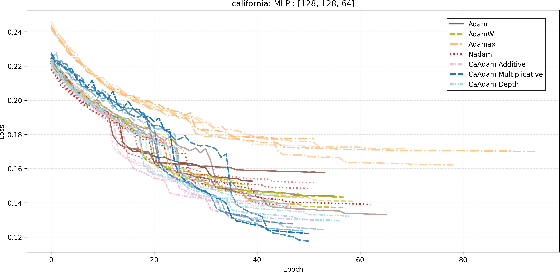
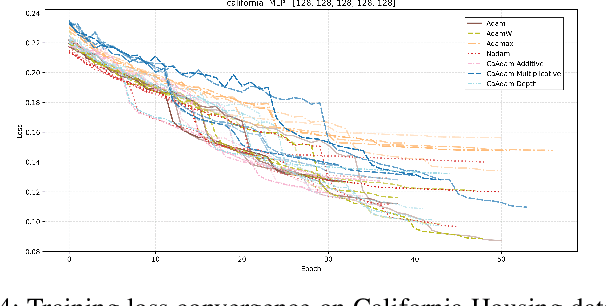
We introduce a new method inspired by Adam that enhances convergence speed and achieves better loss function minima. Traditional optimizers, including Adam, apply uniform or globally adjusted learning rates across neural networks without considering their architectural specifics. This architecture-agnostic approach is deeply embedded in most deep learning frameworks, where optimizers are implemented as standalone modules without direct access to the network's structural information. For instance, in popular frameworks like Keras or PyTorch, optimizers operate solely on gradients and parameters, without knowledge of layer connectivity or network topology. Our algorithm, CaAdam, explores this overlooked area by introducing connection-aware optimization through carefully designed proxies of architectural information. We propose multiple scaling methodologies that dynamically adjust learning rates based on easily accessible structural properties such as layer depth, connection counts, and gradient distributions. This approach enables more granular optimization while working within the constraints of current deep learning frameworks. Empirical evaluations on standard datasets (e.g., CIFAR-10, Fashion MNIST) show that our method consistently achieves faster convergence and higher accuracy compared to standard Adam optimizer, demonstrating the potential benefits of incorporating architectural awareness in optimization strategies.

A Temporal Linear Network for Time Series Forecasting

Recent research has challenged the necessity of complex deep learning architectures for time series forecasting, demonstrating that simple linear models can often outperform sophisticated approaches. Building upon this insight, we introduce a novel architecture the Temporal Linear Net (TLN), that extends the capabilities of linear models while maintaining interpretability and computational efficiency. TLN is designed to effectively capture both temporal and feature-wise dependencies in multivariate time series data. Our approach is a variant of TSMixer that maintains strict linearity throughout its architecture. TSMixer removes activation functions, introduces specialized kernel initializations, and incorporates dilated convolutions to handle various time scales, while preserving the linear nature of the model. Unlike transformer-based models that may lose temporal information due to their permutation-invariant nature, TLN explicitly preserves and leverages the temporal structure of the input data. A key innovation of TLN is its ability to compute an equivalent linear model, offering a level of interpretability not found in more complex architectures such as TSMixer. This feature allows for seamless conversion between the full TLN model and its linear equivalent, facilitating both training flexibility and inference optimization.

SigKAN: Signature-Weighted Kolmogorov-Arnold Networks for Time Series

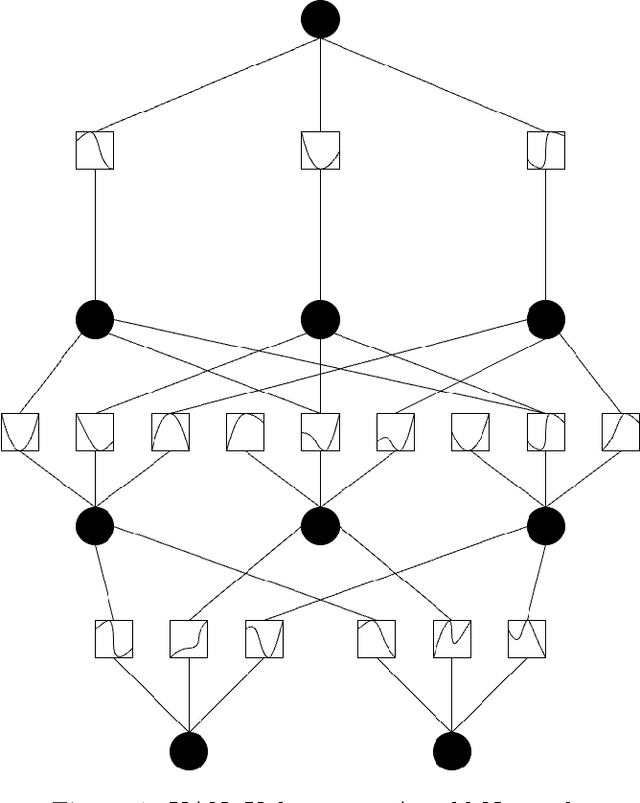
We propose a novel approach that enhances multivariate function approximation using learnable path signatures and Kolmogorov-Arnold networks (KANs). We enhance the learning capabilities of these networks by weighting the values obtained by KANs using learnable path signatures, which capture important geometric features of paths. This combination allows for a more comprehensive and flexible representation of sequential and temporal data. We demonstrate through studies that our SigKANs with learnable path signatures perform better than conventional methods across a range of function approximation challenges. By leveraging path signatures in neural networks, this method offers intriguing opportunities to enhance performance in time series analysis and time series forecasting, among other fields.

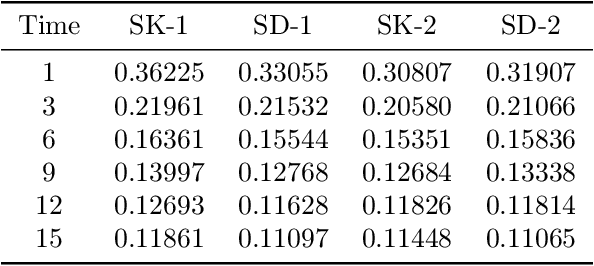
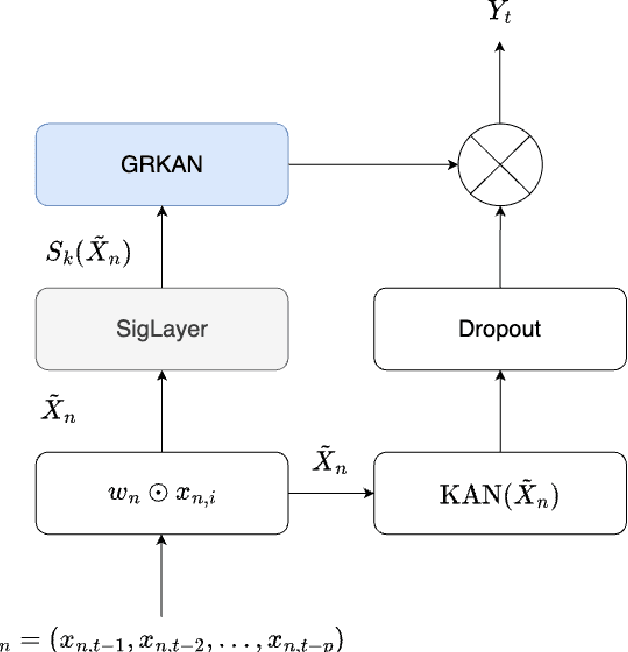
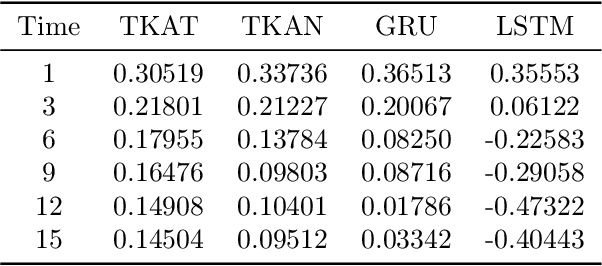
A Temporal Kolmogorov-Arnold Transformer for Time Series Forecasting

Capturing complex temporal patterns and relationships within multivariate data streams is a difficult task. We propose the Temporal Kolmogorov-Arnold Transformer (TKAT), a novel attention-based architecture designed to address this task using Temporal Kolmogorov-Arnold Networks (TKANs). Inspired by the Temporal Fusion Transformer (TFT), TKAT emerges as a powerful encoder-decoder model tailored to handle tasks in which the observed part of the features is more important than the a priori known part. This new architecture combined the theoretical foundation of the Kolmogorov-Arnold representation with the power of transformers. TKAT aims to simplify the complex dependencies inherent in time series, making them more "interpretable". The use of transformer architecture in this framework allows us to capture long-range dependencies through self-attention mechanisms.

TKAN: Temporal Kolmogorov-Arnold Networks

Recurrent Neural Networks (RNNs) have revolutionized many areas of machine learning, particularly in natural language and data sequence processing. Long Short-Term Memory (LSTM) has demonstrated its ability to capture long-term dependencies in sequential data. Inspired by the Kolmogorov-Arnold Networks (KANs) a promising alternatives to Multi-Layer Perceptrons (MLPs), we proposed a new neural networks architecture inspired by KAN and the LSTM, the Temporal Kolomogorov-Arnold Networks (TKANs). TKANs combined the strenght of both networks, it is composed of Recurring Kolmogorov-Arnold Networks (RKANs) Layers embedding memory management. This innovation enables us to perform multi-step time series forecasting with enhanced accuracy and efficiency. By addressing the limitations of traditional models in handling complex sequential patterns, the TKAN architecture offers significant potential for advancements in fields requiring more than one step ahead forecasting.