DLScanner: A parameter space scanner package assisted by deep learning methods

In this paper, we introduce a scanner package enhanced by deep learning (DL) techniques. The proposed package addresses two significant challenges associated with previously developed DL-based methods: slow convergence in high-dimensional scans and the limited generalization of the DL network when mapping random points to the target space. To tackle the first issue, we utilize a similarity learning network that maps sampled points into a representation space. In this space, in-target points are grouped together while out-target points are effectively pushed apart. This approach enhances the scan convergence by refining the representation of sampled points. The second challenge is mitigated by integrating a dynamic sampling strategy. Specifically, we employ a VEGAS mapping to adaptively suggest new points for the DL network while also improving the mapping when more points are collected. Our proposed framework demonstrates substantial gains in both performance and efficiency compared to other scanning methods.

LeStrat-Net: Lebesgue style stratification for Monte Carlo simulations powered by machine learning

We develop a machine learning algorithm to turn around stratification in Monte Carlo sampling. We use a different way to divide the domain space of the integrand, based on the height of the function being sampled, similar to what is done in Lebesgue integration. This means that isocontours of the function define regions that can have any shape depending on the behavior of the function. We take advantage of the capacity of neural networks to learn complicated functions in order to predict these complicated divisions and preclassify large samples of the domain space. From this preclassification we can select the required number of points to perform a number of tasks such as variance reduction, integration and even event selection. The network ultimately defines the regions with what it learned and is also used to calculate the multi-dimensional volume of each region.

Exploration of Parameter Spaces Assisted by Machine Learning

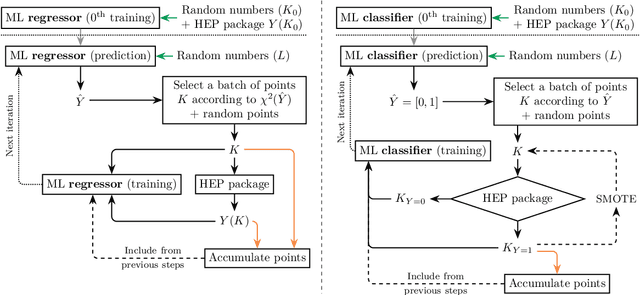
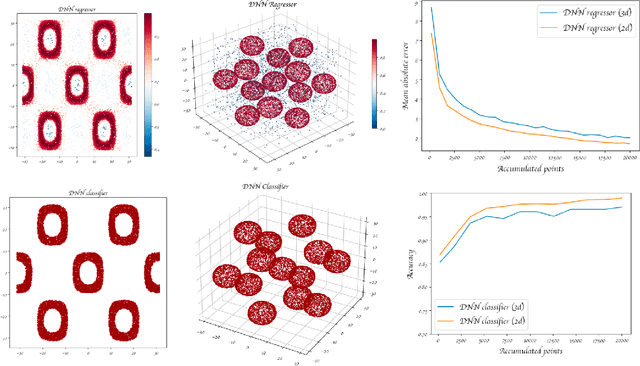
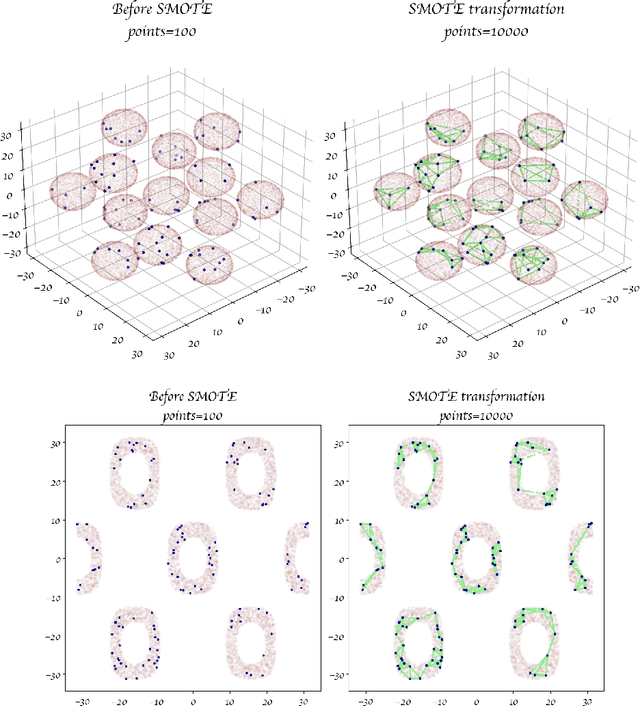
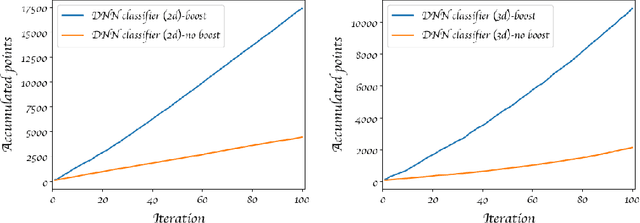
We showcase a variety of functions and classes that implement sampling procedures with improved exploration of the parameter space assisted by machine learning. Special attention is paid to setting sane defaults with the objective that adjustments required by different problems remain minimal. This collection of routines can be employed for different types of analysis, from finding bounds on the parameter space to accumulating samples in areas of interest. In particular, we discuss two methods assisted by incorporating different machine learning models: regression and classification. We show that a machine learning classifier can provide higher efficiency for exploring the parameter space. Also, we introduce a boosting technique to improve the slow convergence at the start of the process. The use of these routines is better explained with the help of a few examples that illustrate the type of results one can obtain. We also include examples of the code used to obtain the examples as well as descriptions of the adjustments that can be made to adapt the calculation to other problems. We finalize by showing the impact of these techniques when exploring the parameter space of the two Higgs doublet model that matches the measured Higgs Boson signal strength. The code used for this paper and instructions on how to use it are available on the web.