Re-Envisioning Numerical Information Field Theory (NIFTy.re): A Library for Gaussian Processes and Variational Inference

Imaging is the process of transforming noisy, incomplete data into a space that humans can interpret. NIFTy is a Bayesian framework for imaging and has already successfully been applied to many fields in astrophysics. Previous design decisions held the performance and the development of methods in NIFTy back. We present a rewrite of NIFTy, coined NIFTy.re, which reworks the modeling principle, extends the inference strategies, and outsources much of the heavy lifting to JAX. The rewrite dramatically accelerates models written in NIFTy, lays the foundation for new types of inference machineries, improves maintainability, and enables interoperability between NIFTy and the JAX machine learning ecosystem.

Attention to Entropic Communication

The concept of attention, numerical weights that emphasize the importance of particular data, has proven to be very relevant in artificial intelligence. Relative entropy (RE, aka Kullback-Leibler divergence) plays a central role in communication theory. Here we combine these concepts, attention and RE. RE guides optimal encoding of messages in bandwidth-limited communication as well as optimal message decoding via the maximum entropy principle (MEP). In the coding scenario, RE can be derived from four requirements, namely being analytical, local, proper, and calibrated. Weighted RE, used for attention steering in communications, turns out to be improper. To see how proper attention communication can emerge, we analyze a scenario of a message sender who wants to ensure that the receiver of the message can perform well-informed actions. If the receiver decodes the message using the MEP, the sender only needs to know the receiver's utility function to inform optimally, but not the receiver's initial knowledge state. In case only the curvature of the utility function maxima are known, it becomes desirable to accurately communicate an attention function, in this case a by this curvature weighted and re-normalized probability function. Entropic attention communication is here proposed as the desired generalization of entropic communication that permits weighting while being proper, thereby aiding the design of optimal communication protocols in technical applications and helping to understand human communication. For example, our analysis shows how to derive the level of cooperation expected under misaligned interests of otherwise honest communication partners.

Sparse Kernel Gaussian Processes through Iterative Charted Refinement (ICR)

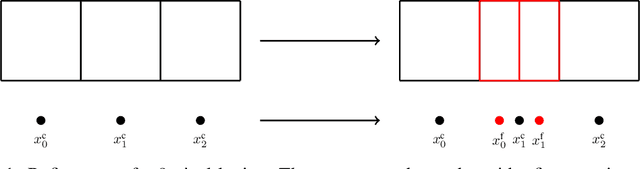
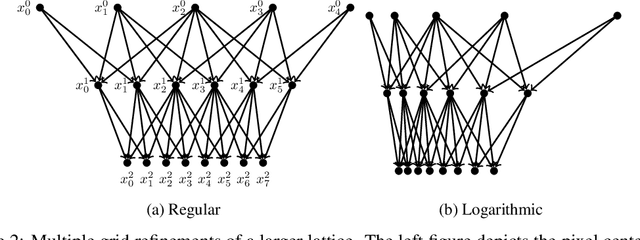
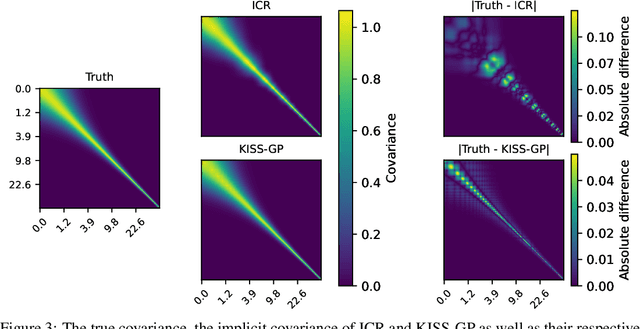
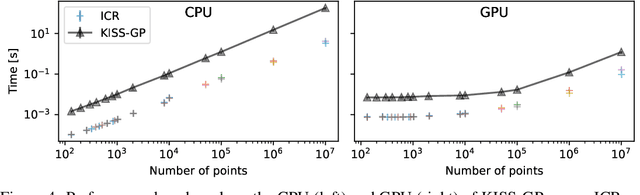
Gaussian Processes (GPs) are highly expressive, probabilistic models. A major limitation is their computational complexity. Naively, exact GP inference requires $\mathcal{O}(N^3)$ computations with $N$ denoting the number of modeled points. Current approaches to overcome this limitation either rely on sparse, structured or stochastic representations of data or kernel respectively and usually involve nested optimizations to evaluate a GP. We present a new, generative method named Iterative Charted Refinement (ICR) to model GPs on nearly arbitrarily spaced points in $\mathcal{O}(N)$ time for decaying kernels without nested optimizations. ICR represents long- as well as short-range correlations by combining views of the modeled locations at varying resolutions with a user-provided coordinate chart. In our experiment with points whose spacings vary over two orders of magnitude, ICR's accuracy is comparable to state-of-the-art GP methods. ICR outperforms existing methods in terms of computational speed by one order of magnitude on the CPU and GPU and has already been successfully applied to model a GP with $122$ billion parameters.

Probabilistic Autoencoder using Fisher Information

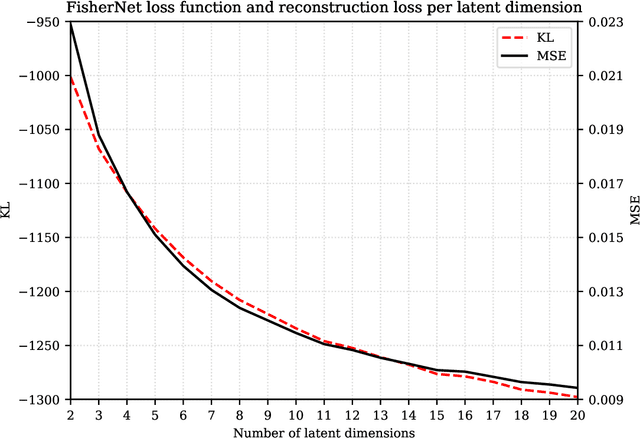
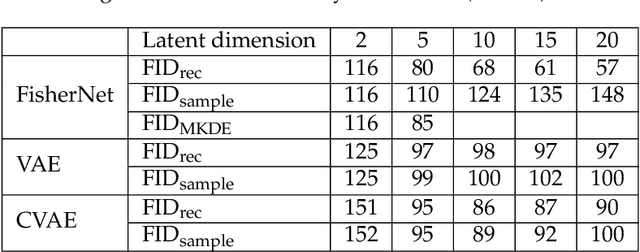
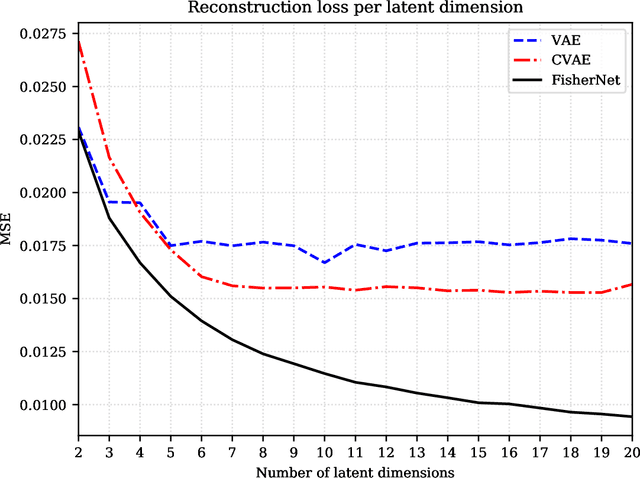
Neural Networks play a growing role in many science disciplines, including physics. Variational Autoencoders (VAEs) are neural networks that are able to represent the essential information of a high dimensional data set in a low dimensional latent space, which have a probabilistic interpretation. In particular the so-called encoder network, the first part of the VAE, which maps its input onto a position in latent space, additionally provides uncertainty information in terms of a variance around this position. In this work, an extension to the Autoencoder architecture is introduced, the FisherNet. In this architecture, the latent space uncertainty is not generated using an additional information channel in the encoder, but derived from the decoder, by means of the Fisher information metric. This architecture has advantages from a theoretical point of view as it provides a direct uncertainty quantification derived from the model, and also accounts for uncertainty cross-correlations. We can show experimentally that the FisherNet produces more accurate data reconstructions than a comparable VAE and its learning performance also apparently scales better with the number of latent space dimensions.

Non-parametric Bayesian Causal Modeling of the SARS-CoV-2 Viral Load Distribution vs. Patient's Age

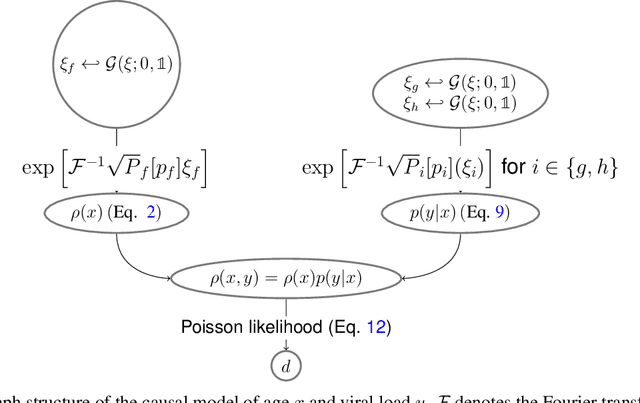
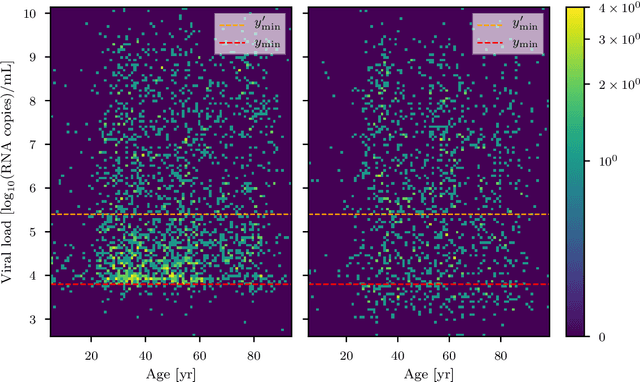
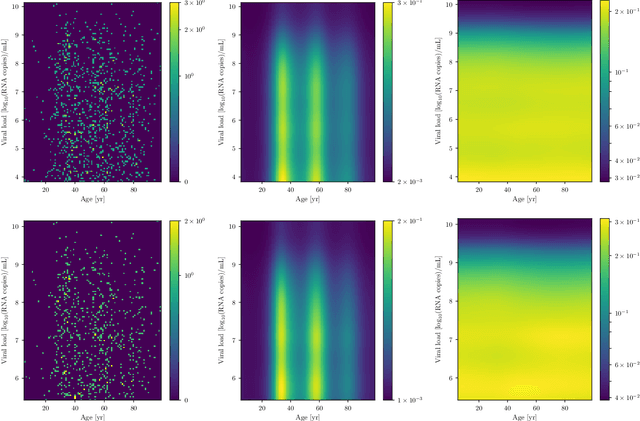
The viral load of patients infected with SARS-CoV-2 varies on logarithmic scales and possibly with age. Controversial claims have been made in the literature regarding whether the viral load distribution actually depends on the age of the patients. Such a dependence would have implications for the COVID-19 spreading mechanism, the age-dependent immune system reaction, and thus for policymaking. We hereby develop a method to analyze viral-load distribution data as a function of the patients' age within a flexible, non-parametric, hierarchical, Bayesian, and causal model. This method can be applied to other contexts as well, and for this purpose, it is made freely available. The developed reconstruction method also allows testing for bias in the data. This could be due to, e.g., bias in patient-testing and data collection or systematic errors in the measurement of the viral load. We perform these tests by calculating the Bayesian evidence for each implied possible causal direction. When applying these tests to publicly available age and SARS-CoV-2 viral load data, we find a statistically significant increase in the viral load with age, but only for one of the two analyzed datasets. If we consider this dataset, and based on the current understanding of viral load's impact on patients' infectivity, we expect a non-negligible difference in the infectivity of different age groups. This difference is nonetheless too small to justify considering any age group as noninfectious.

Geometric variational inference

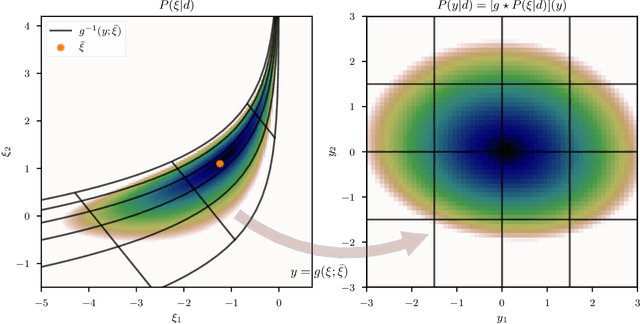
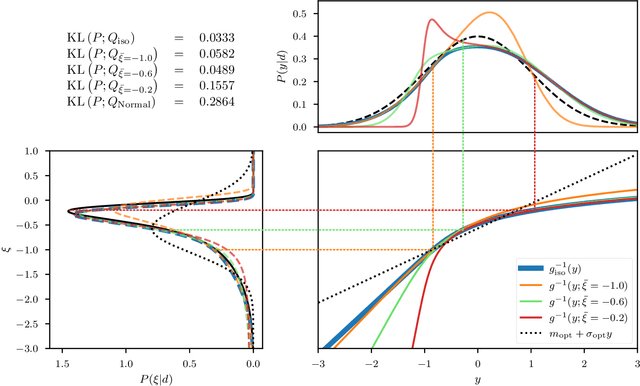
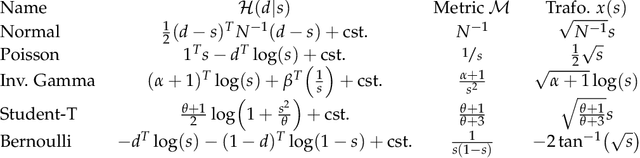
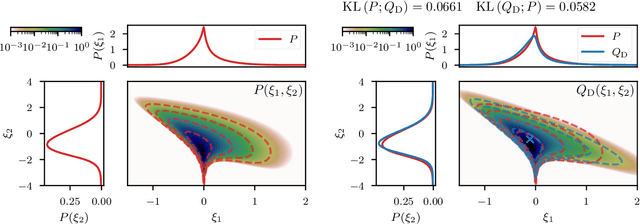
Efficiently accessing the information contained in non-linear and high dimensional probability distributions remains a core challenge in modern statistics. Traditionally, estimators that go beyond point estimates are either categorized as Variational Inference (VI) or Markov-Chain Monte-Carlo (MCMC) techniques. While MCMC methods that utilize the geometric properties of continuous probability distributions to increase their efficiency have been proposed, VI methods rarely use the geometry. This work aims to fill this gap and proposes geometric Variational Inference (geoVI), a method based on Riemannian geometry and the Fisher information metric. It is used to construct a coordinate transformation that relates the Riemannian manifold associated with the metric to Euclidean space. The distribution, expressed in the coordinate system induced by the transformation, takes a particularly simple form that allows for an accurate variational approximation by a normal distribution. Furthermore, the algorithmic structure allows for an efficient implementation of geoVI which is demonstrated on multiple examples, ranging from low-dimensional illustrative ones to non-linear, hierarchical Bayesian inverse problems in thousands of dimensions.