pyhgf: A neural network library for predictive coding

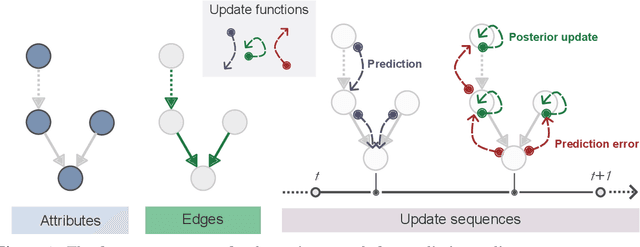
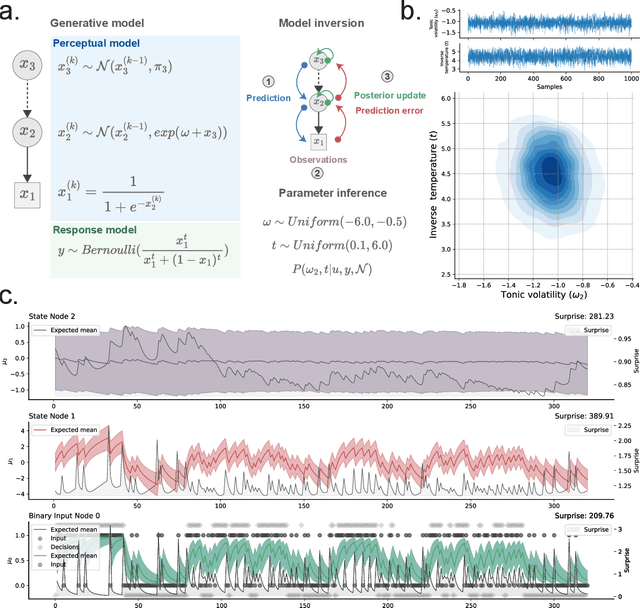
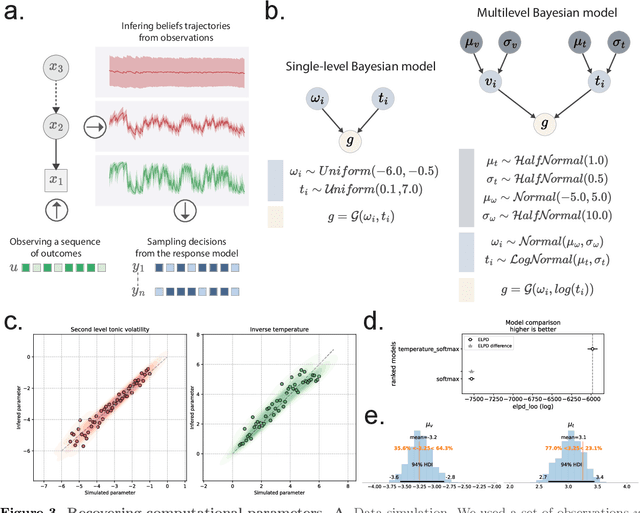
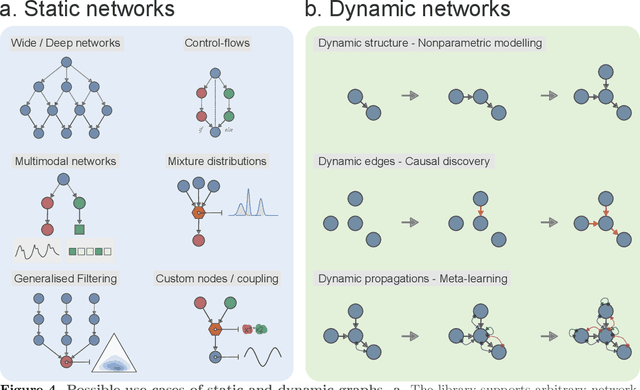
Bayesian models of cognition have gained considerable traction in computational neuroscience and psychiatry. Their scopes are now expected to expand rapidly to artificial intelligence, providing general inference frameworks to support embodied, adaptable, and energy-efficient autonomous agents. A central theory in this domain is predictive coding, which posits that learning and behaviour are driven by hierarchical probabilistic inferences about the causes of sensory inputs. Biological realism constrains these networks to rely on simple local computations in the form of precision-weighted predictions and prediction errors. This can make this framework highly efficient, but its implementation comes with unique challenges on the software development side. Embedding such models in standard neural network libraries often becomes limiting, as these libraries' compilation and differentiation backends can force a conceptual separation between optimization algorithms and the systems being optimized. This critically departs from other biological principles such as self-monitoring, self-organisation, cellular growth and functional plasticity. In this paper, we introduce \texttt{pyhgf}: a Python package backed by JAX and Rust for creating, manipulating and sampling dynamic networks for predictive coding. We improve over other frameworks by enclosing the network components as transparent, modular and malleable variables in the message-passing steps. The resulting graphs can implement arbitrary computational complexities as beliefs propagation. But the transparency of core variables can also translate into inference processes that leverage self-organisation principles, and express structure learning, meta-learning or causal discovery as the consequence of network structural adaptation to surprising inputs. The code, tutorials and documentation are hosted at: https://github.com/ilabcode/pyhgf.

The generalized Hierarchical Gaussian Filter

Hierarchical Bayesian models of perception and learning feature prominently in contemporary cognitive neuroscience where, for example, they inform computational concepts of mental disorders. This includes predictive coding and hierarchical Gaussian filtering (HGF), which differ in the nature of hierarchical representations. Predictive coding assumes that higher levels in a given hierarchy influence the state (value) of lower levels. In HGF, however, higher levels determine the rate of change at lower levels. Here, we extend the space of generative models underlying HGF to include a form of nonlinear hierarchical coupling between state values akin to predictive coding and artificial neural networks in general. We derive the update equations corresponding to this generalization of HGF and conceptualize them as connecting a network of (belief) nodes where parent nodes either predict the state of child nodes or their rate of change. This enables us to (1) create modular architectures with generic computational steps in each node of the network, and (2) disclose the hierarchical message passing implied by generalized HGF models and to compare this to comparable schemes under predictive coding. We find that the algorithmic architecture instantiated by the generalized HGF is largely compatible with that of predictive coding but extends it with some unique predictions which arise from precision and volatility related computations. Our developments enable highly flexible implementations of hierarchical Bayesian models for empirical data analysis and are available as open source software.