Robust Matrix Elastic Net based Canonical Correlation Analysis: An Effective Algorithm for Multi-View Unsupervised Learning

This paper presents a robust matrix elastic net based canonical correlation analysis (RMEN-CCA) for multiple view unsupervised learning problems, which emphasizes the combination of CCA and the robust matrix elastic net (RMEN) used as coupled feature selection. The RMEN-CCA leverages the strength of the RMEN to distill naturally meaningful features without any prior assumption and to measure effectively correlations between different 'views'. We can further employ directly the kernel trick to extend the RMEN-CCA to the kernel scenario with theoretical guarantees, which takes advantage of the kernel trick for highly complicated nonlinear feature learning. Rather than simply incorporating existing regularization minimization terms into CCA, this paper provides a new learning paradigm for CCA and is the first to derive a coupled feature selection based CCA algorithm that guarantees convergence. More significantly, for CCA, the newly-derived RMEN-CCA bridges the gap between measurement of relevance and coupled feature selection. Moreover, it is nontrivial to tackle directly the RMEN-CCA by previous optimization approaches derived from its sophisticated model architecture. Therefore, this paper further offers a bridge between a new optimization problem and an existing efficient iterative approach. As a consequence, the RMEN-CCA can overcome the limitation of CCA and address large-scale and streaming data problems. Experimental results on four popular competing datasets illustrate that the RMEN-CCA performs more effectively and efficiently than do state-of-the-art approaches.

A New Learning Paradigm for Random Vector Functional-Link Network: RVFL+

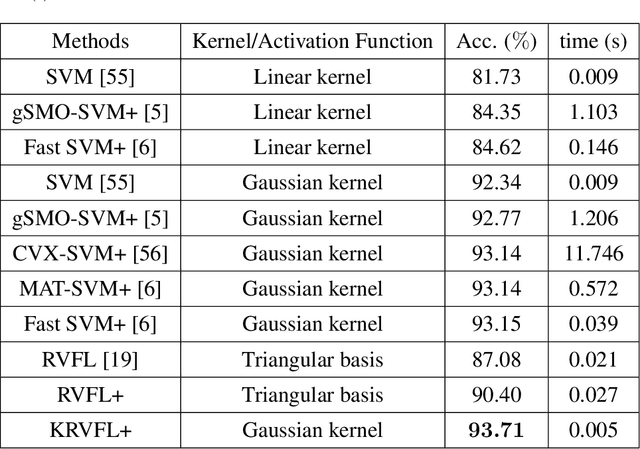
In school, a teacher plays an important role in various classroom teaching patterns. Likewise to this human learning activity, the learning using privileged information (LUPI) paradigm provides additional information generated by the teacher to 'teach' learning algorithms during the training stage. Therefore, this novel learning paradigm is a typical Teacher-Student Interaction mechanism. This paper is the first to present a random vector functional link network based on the LUPI paradigm, called RVFL+. Rather than simply combining two existing approaches, the newly-derived RVFL+ fills the gap between neural networks and the LUPI paradigm, which offers an alternative way to train RVFL networks. Moreover, the proposed RVFL+ can perform in conjunction with the kernel trick for highly complicated nonlinear feature learning, which is termed KRVFL+. Furthermore, the statistical property of the proposed RVFL+ is investigated, and we derive a sharp and high-quality generalization error bound based on the Rademacher complexity. Competitive experimental results on 14 real-world datasets illustrate the great effectiveness and efficiency of the novel RVFL+ and KRVFL+, which can achieve better generalization performance than state-of-the-art algorithms.