Peder Harderup
Differential Flatness and Flatness Inspired Control of Aerial Manipulators based on Lagrangian Reduction
Nov 02, 2021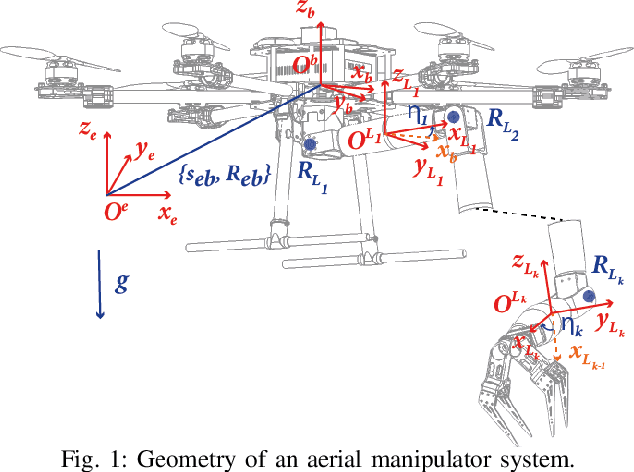
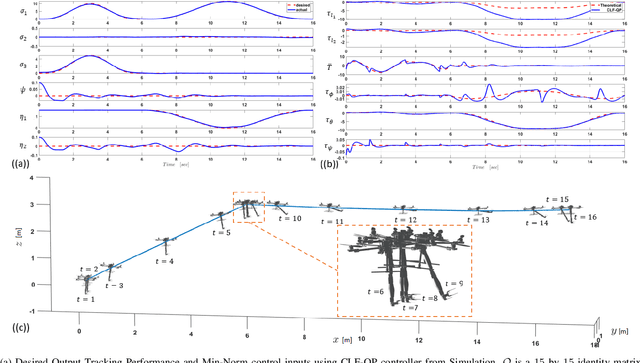
Abstract:This paper shows that the dynamics of a general class of aerial manipulators, consist of an underactuated multi-rotor base with an arbitrary k-linked articulated manipulator, are differentially flat. Methods of Lagrangian Reduction under broken symmetries produce reduced equations of motion whose key variables: center-of-mass linear momentum, vehicle yaw angle, and manipulator relative joint angles become the flat outputs. Utilizing flatness theory and a second-order dynamic extension of the thrust input, we transform the mechanics of aerial manipulators to their equivalent trivial form with a valid relative degree. Using this flatness transformation, a quadratic programming-based controller is proposed within a Control Lyapunov Function (CLF-QP) framework, and its performance is verified in simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge