Predicting Air Temperature from Volumetric Urban Morphology with Machine Learning

In this study, we firstly introduce a method that converts CityGML data into voxels which works efficiently and fast in high resolution for large scale datasets such as cities but by sacrificing some building details to overcome the limitations of previous voxelization methodologies that have been computationally intensive and inefficient at transforming large-scale urban areas into voxel representations for high resolution. Those voxelized 3D city data from multiple cities and corresponding air temperature data are used to develop a machine learning model. Before the model training, Gaussian blurring is implemented on input data to consider spatial relationships, as a result the correlation rate between air temperature and volumetric building morphology is also increased after the Gaussian blurring. After the model training, the prediction results are not just evaluated with Mean Square Error (MSE) but some image similarity metrics such as Structural Similarity Index Measure (SSIM) and Learned Perceptual Image Patch Similarity (LPIPS) that are able to detect and consider spatial relations during the evaluation process. This trained model is capable of predicting the spatial distribution of air temperature by using building volume information of corresponding pixel as input. By doing so, this research aims to assist urban planners in incorporating environmental parameters into their planning strategies, thereby facilitating more sustainable and inhabitable urban environments.

On the Local Ultrametricity of Finite Metric Data

New local ultrametricity measures for finite metric data are proposed through the viewpoint that their Vietoris-Rips corners are samples from p-adic Mumford curves endowed with a Radon measure coming from a regular differential 1-form. This is experimentally applied to the iris dataset.

A $p$-adic RanSaC algorithm for stereo vision using Hensel lifting

A $p$-adic variation of the Ran(dom) Sa(mple) C(onsensus) method for solving the relative pose problem in stereo vision is developped. From two 2-adically encoded images a random sample of five pairs of corresponding points is taken, and the equations for the essential matrix are solved by lifting solutions modulo 2 to the 2-adic integers. A recently devised $p$-adic hierarchical classification algorithm imitating the known LBG quantisation method classifies the solutions for all the samples after having determined the number of clusters using the known intra-inter validity of clusterings. In the successful case, a cluster ranking will determine the cluster containing a 2-adic approximation to the "true" solution of the problem.

A dyadic solution of relative pose problems

A hierarchical interval subdivision is shown to lead to a $p$-adic encoding of image data. This allows in the case of the relative pose problem in computer vision and photogrammetry to derive equations having 2-adic numbers as coefficients, and to use Hensel's lifting method to their solution. This method is applied to the linear and non-linear equations coming from eight, seven or five point correspondences. An inherent property of the method is its robustness.

On $p$-adic Classification

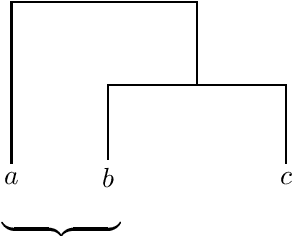
A $p$-adic modification of the split-LBG classification method is presented in which first clusterings and then cluster centers are computed which locally minimise an energy function. The outcome for a fixed dataset is independent of the prime number $p$ with finitely many exceptions. The methods are applied to the construction of $p$-adic classifiers in the context of learning.

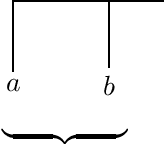
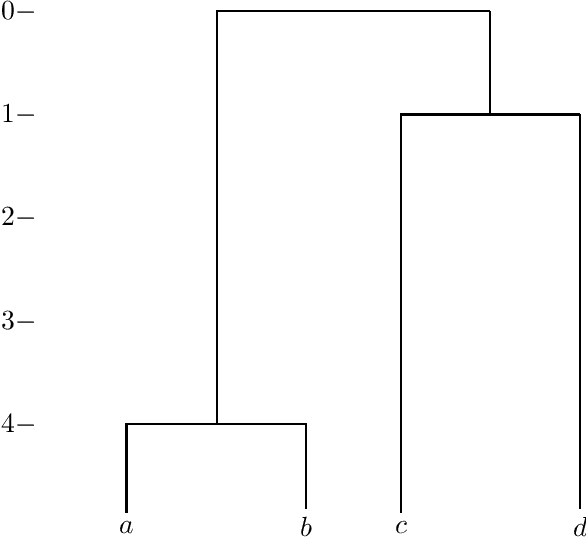
Families of dendrograms

A conceptual framework for cluster analysis from the viewpoint of p-adic geometry is introduced by describing the space of all dendrograms for n datapoints and relating it to the moduli space of p-adic Riemannian spheres with punctures using a method recently applied by Murtagh (2004b). This method embeds a dendrogram as a subtree into the Bruhat-Tits tree associated to the p-adic numbers, and goes back to Cornelissen et al. (2001) in p-adic geometry. After explaining the definitions, the concept of classifiers is discussed in the context of moduli spaces, and upper bounds for the number of hidden vertices in dendrograms are given.

Degenerating families of dendrograms

Dendrograms used in data analysis are ultrametric spaces, hence objects of nonarchimedean geometry. It is known that there exist $p$-adic representation of dendrograms. Completed by a point at infinity, they can be viewed as subtrees of the Bruhat-Tits tree associated to the $p$-adic projective line. The implications are that certain moduli spaces known in algebraic geometry are $p$-adic parameter spaces of (families of) dendrograms, and stochastic classification can also be handled within this framework. At the end, we calculate the topology of the hidden part of a dendrogram.