RAIN-FIT: Learning of Fitting Surfaces and Noise Distribution from Large Data Sets

This paper proposes a method for estimating a surface that contains a given set of points from noisy measurements. More precisely, by assuming that the surface is described by the zero set of a function in the span of a given set of features and a parametric description of the distribution of the noise, a computationally efficient method is described that estimates both the surface and the noise distribution parameters. In the provided examples, polynomial and sinusoidal basis functions were used. However, any chosen basis that satisfies the outlined conditions mentioned in the paper can be approximated as a combination of trigonometric, exponential, and/or polynomial terms, making the presented approach highly generalizable. The proposed algorithm exhibits linear computational complexity in the number of samples. Our approach requires no hyperparameter tuning or data preprocessing and effectively handles data in dimensions beyond 2D and 3D. The theoretical results demonstrating the convergence of the proposed algorithm have been provided. To highlight the performance of the proposed method, comprehensive numerical results are conducted, evaluating our method against state-of-the-art algorithms, including Poisson Reconstruction and the Neural Network-based Encoder-X, on 2D and 3D shapes. The results demonstrate the superiority of our method under the same conditions.

Unsupervised Learning for Pilot-free Transmission in 3GPP MIMO Systems

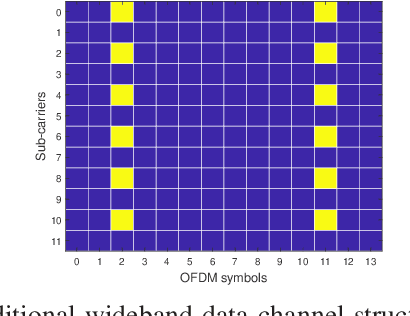
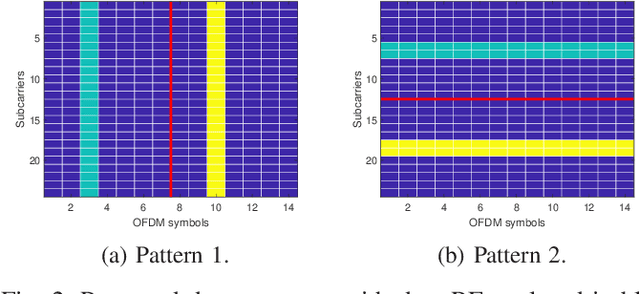
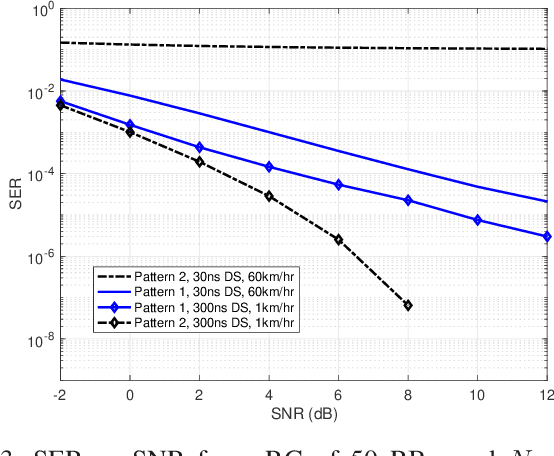
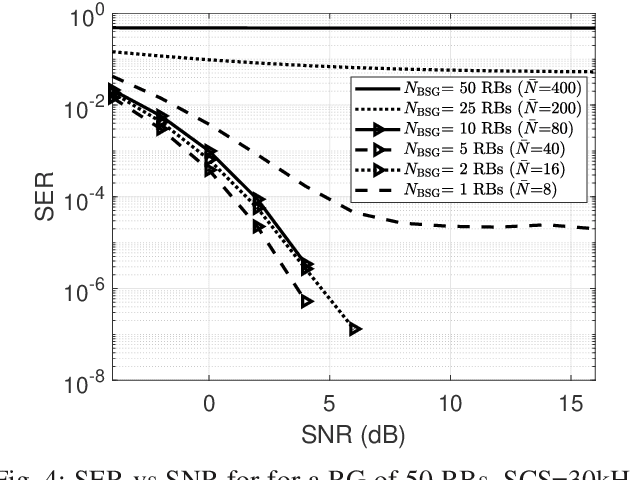
Reference signals overhead reduction has recently evolved as an effective solution for improving the system spectral efficiency. This paper introduces a new downlink data structure that is free from demodulation reference signals (DM-RS), and hence does not require any channel estimation at the receiver. The new proposed data transmission structure involves a simple repetition step of part of the user data across the different sub-bands. Exploiting the repetition structure at the user side, it is shown that reliable recovery is possible via canonical correlation analysis. This paper also proposes two effective mechanisms for boosting the CCA performance in OFDM systems; one for repetition pattern selection and another to deal with the severe frequency selectivity issues. The proposed approach exhibits favorable complexity-performance tradeoff, rendering it appealing for practical implementation. Numerical results, using a 3GPP link-level testbench, demonstrate the superiority of the proposed approach relative to the state-of-the-art methods.

Lp Quasi-norm Minimization: Algorithm and Applications

Sparsity finds applications in areas as diverse as statistics, machine learning, and signal processing. Computations over sparse structures are less complex compared to their dense counterparts, and their storage consumes less space. This paper proposes a heuristic method for retrieving sparse approximate solutions of optimization problems via minimizing the $\ell_{p}$ quasi-norm, where $0<p<1$. An iterative two-block ADMM algorithm for minimizing the $\ell_{p}$ quasi-norm subject to convex constraints is proposed. For $p=s/q<1$, $s,q \in \mathbb{Z}_{+}$, the proposed algorithm requires solving for the roots of a scalar degree $2q$ polynomial as opposed to applying a soft thresholding operator in the case of $\ell_{1}$. The merit of that algorithm relies on its ability to solve the $\ell_{p}$ quasi-norm minimization subject to any convex set of constraints. However, it suffers from low speed, due to a convex projection step in each iteration, and the lack of mathematical convergence guarantee. We then aim to vanquish these shortcomings by relaxing the assumption on the constraints set to be the set formed due to convex and differentiable, with Lipschitz continuous gradient, functions, i.e. specifically, polytope sets. Using a proximal gradient step, we mitigate the convex projection step and hence enhance the algorithm speed while proving its convergence. We then present various applications where the proposed algorithm excels, namely, matrix rank minimization, sparse signal reconstruction from noisy measurements, sparse binary classification, and system identification. The results demonstrate the significant gains obtained by the proposed algorithm compared to those via $\ell_{1}$ minimization.