A logic for reasoning with inconsistent knowledge -- A reformulation using nowadays terminology (2024)

In many situations humans have to reason with inconsistent knowledge. These inconsistencies may occur due to not fully reliable sources of information. In order to reason with inconsistent knowledge, it is not possible to view a set of premisses as absolute truths as is done in predicate logic. Viewing the set of premisses as a set of assumptions, however, it is possible to deduce useful conclusions from an inconsistent set of premisses. In this paper a logic for reasoning with inconsistent knowledge is described. This logic is a generalization of the work of N. Rescher [15]. In the logic a reliability relation is used to choose between incompatible assumptions. These choices are only made when a contradiction is derived. As long as no contradiction is derived, the knowledge is assumed to be consistent. This makes it possible to define an argumentation-based deduction process for the logic. For the logic a semantics based on the ideas of Y. Shoham [22, 23], is defined. It turns out that the semantics for the logic is a preferential semantics according to the definition S. Kraus, D. Lehmann and M. Magidor [12]. Therefore the logic is a logic of system P and possesses all the properties of an ideal non-monotonic logic.

On resolving conflicts between arguments

Argument systems are based on the idea that one can construct arguments for propositions; i.e., structured reasons justifying the belief in a proposition. Using defeasible rules, arguments need not be valid in all circumstances, therefore, it might be possible to construct an argument for a proposition as well as its negation. When arguments support conflicting propositions, one of the arguments must be defeated, which raises the question of \emph{which (sub-)arguments can be subject to defeat}? In legal argumentation, meta-rules determine the valid arguments by considering the last defeasible rule of each argument involved in a conflict. Since it is easier to evaluate arguments using their last rules, \emph{can a conflict be resolved by considering only the last defeasible rules of the arguments involved}? We propose a new argument system where, instead of deriving a defeat relation between arguments, \emph{undercutting-arguments} for the defeat of defeasible rules are constructed. This system allows us, (\textit{i}) to resolve conflicts (a generalization of rebutting arguments) using only the last rules of the arguments for inconsistencies, (\textit{ii}) to determine a set of valid (undefeated) arguments in linear time using an algorithm based on a JTMS, (\textit{iii}) to establish a relation with Default Logic, and (\textit{iv}) to prove closure properties such as \emph{cumulativity}. We also propose an extension of the argument system that enables \emph{reasoning by cases}.

Efficient Model Based Diagnosis

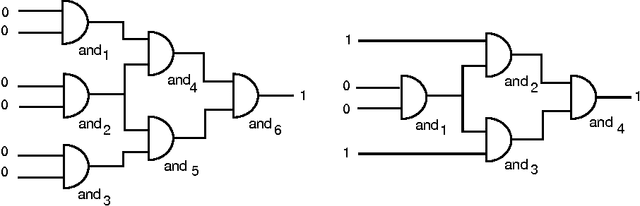
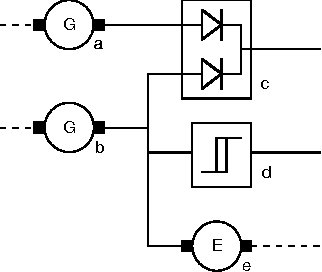
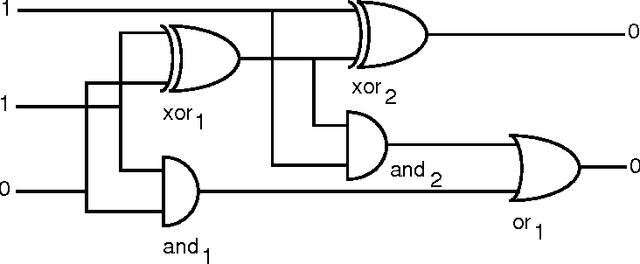
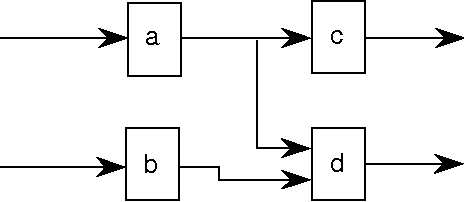
In this paper an efficient model based diagnostic process is described for systems whose components possess a causal relation between their inputs and their outputs. In this diagnostic process, firstly, a set of focuses on likely broken components is determined. Secondly, for each focus the most informative probing point within the focus can be determined. Both these steps of the diagnostic process have a worst case time complexity of ${\cal O}(n^2)$ where $n$ is the number of components. If the connectivity of the components is low, however, the diagnostic process shows a linear time complexity. It is also shown how the diagnostic process described can be applied in dynamic systems and systems containing loops. When diagnosing dynamic systems it is possible to choose between detecting intermitting faults or to improve the diagnostic precision by assuming non-intermittency.

A Semantic Tableau Method for Argument Construction

A semantic tableau method, called an argumentation tableau, that enables the derivation of arguments, is proposed. First, the derivation of arguments for standard propositional and predicate logic is addressed. Next, an extension that enables reasoning with defeasible rules is presented. Finally, reasoning by cases using an argumentation tableau is discussed.

Explainable AI through the Learning of Arguments

Learning arguments is highly relevant to the field of explainable artificial intelligence. It is a family of symbolic machine learning techniques that is particularly human-interpretable. These techniques learn a set of arguments as an intermediate representation. Arguments are small rules with exceptions that can be chained to larger arguments for making predictions or decisions. We investigate the learning of arguments, specifically the learning of arguments from a 'case model' proposed by Verheij [34]. The case model in Verheij's approach are cases or scenarios in a legal setting. The number of cases in a case model are relatively low. Here, we investigate whether Verheij's approach can be used for learning arguments from other types of data sets with a much larger number of instances. We compare the learning of arguments from a case model with the HeRO algorithm [15] and learning a decision tree.

An argumentation system for reasoning with conflict-minimal paraconsistent ALC

The semantic web is an open and distributed environment in which it is hard to guarantee consistency of knowledge and information. Under the standard two-valued semantics everything is entailed if knowledge and information is inconsistent. The semantics of the paraconsistent logic LP offers a solution. However, if the available knowledge and information is consistent, the set of conclusions entailed under the three-valued semantics of the paraconsistent logic LP is smaller than the set of conclusions entailed under the two-valued semantics. Preferring conflict-minimal three-valued interpretations eliminates this difference. Preferring conflict-minimal interpretations introduces non-monotonicity. To handle the non-monotonicity, this paper proposes an assumption-based argumentation system. Assumptions needed to close branches of a semantic tableaux form the arguments. Stable extensions of the set of derived arguments correspond to conflict minimal interpretations and conclusions entailed by all conflict-minimal interpretations are supported by arguments in all stable extensions.