Nguyen Duc Thai
A bi-level encoding scheme for the clustered shortest-path tree problem in multifactorial optimization
Feb 12, 2021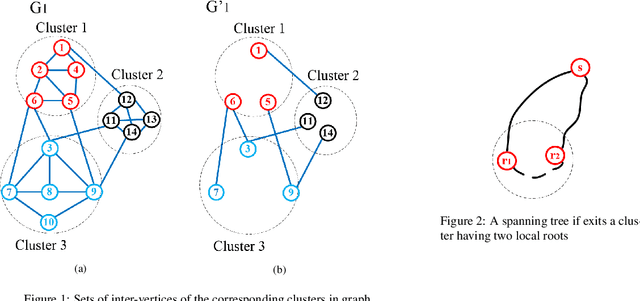

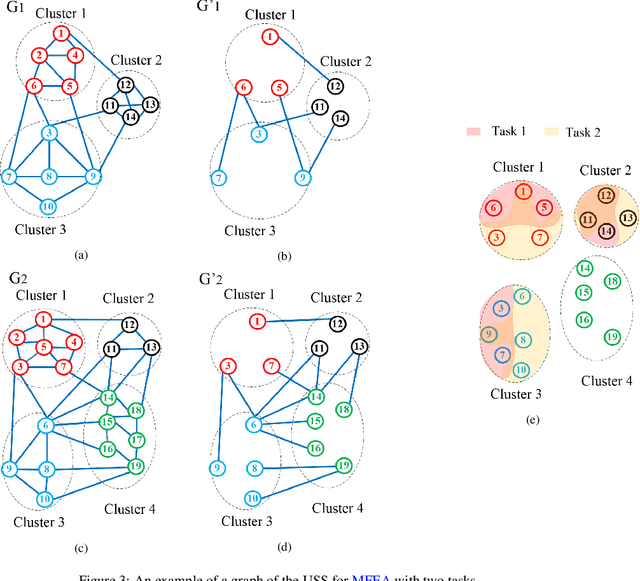
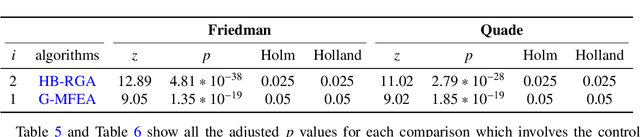
Abstract:The Clustered Shortest-Path Tree Problem (CluSPT) plays an important role in various types of optimization problems in real-life. Recently, some Multifactorial Evolutionary Algorithm (MFEA) have been introduced to deal with the CluSPT, however these researches still have some shortcomings such as evolution operators only perform on complete graphs, huge resource consumption for finding the solution on large search spaces. To overcome these limitations, this paper describes a MFEA-based approach to solve the CluSPT. The proposed algorithm utilizes Dijkstra's algorithm to construct the spanning trees in clusters while using evolutionary operators for building the spanning tree connecting clusters. This approach takes advantage of both exact and approximate algorithms so it enables the algorithm to function efficiently on complete and sparse graphs alike. Furthermore, evolutionary operators such as individual encoding and decoding methods are also designed with great consideration regarding performance and memory usage. We have included a proof on the repairing method's efficacy in ensuring all solutions are valid. We have conducted tests on various types of Euclidean instances to assess the effectiveness of the proposed algorithm and methods. Experiment results point out the effectiveness of the proposed algorithm existing heuristic algorithms in most of the test cases. The impact of the proposed MFEA was analyzed and a possible influential factor that may be useful for further study was also pointed out.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge