N. T. Hunt-Smith
Accelerating Markov Chain Monte Carlo sampling with diffusion models
Sep 04, 2023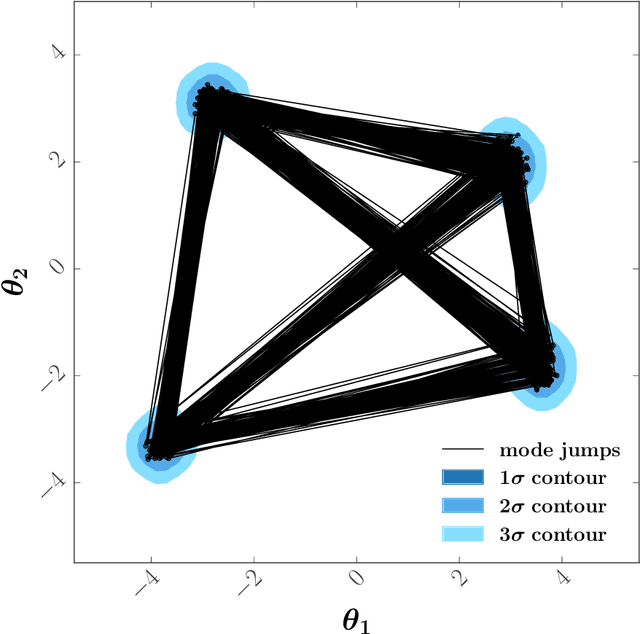
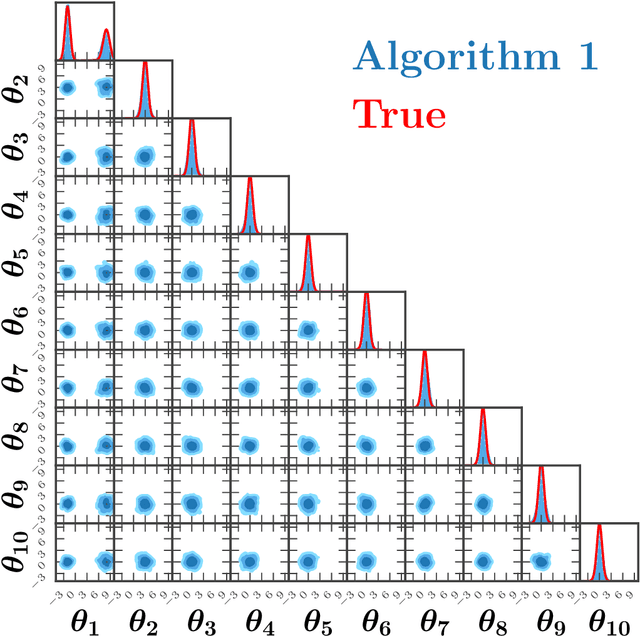
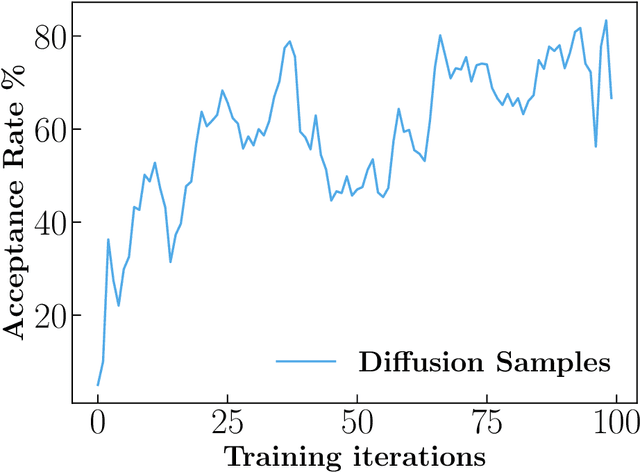
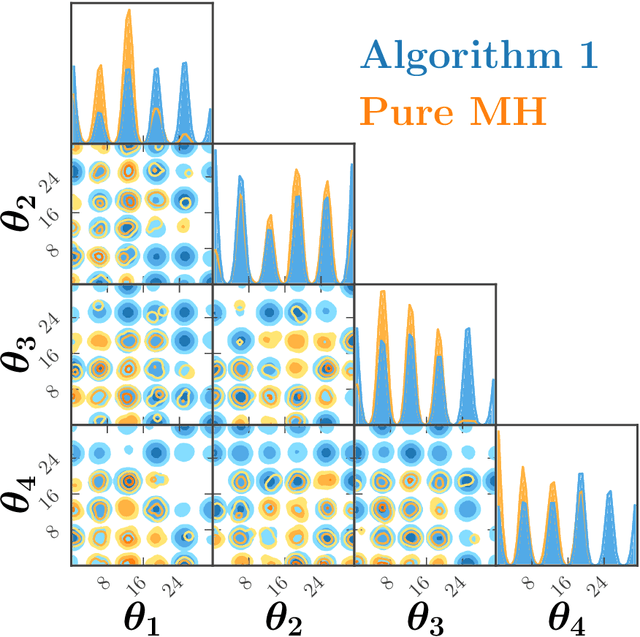
Abstract:Global fits of physics models require efficient methods for exploring high-dimensional and/or multimodal posterior functions. We introduce a novel method for accelerating Markov Chain Monte Carlo (MCMC) sampling by pairing a Metropolis-Hastings algorithm with a diffusion model that can draw global samples with the aim of approximating the posterior. We briefly review diffusion models in the context of image synthesis before providing a streamlined diffusion model tailored towards low-dimensional data arrays. We then present our adapted Metropolis-Hastings algorithm which combines local proposals with global proposals taken from a diffusion model that is regularly trained on the samples produced during the MCMC run. Our approach leads to a significant reduction in the number of likelihood evaluations required to obtain an accurate representation of the Bayesian posterior across several analytic functions, as well as for a physical example based on a global analysis of parton distribution functions. Our method is extensible to other MCMC techniques, and we briefly compare our method to similar approaches based on normalizing flows. A code implementation can be found at https://github.com/NickHunt-Smith/MCMC-diffusion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge