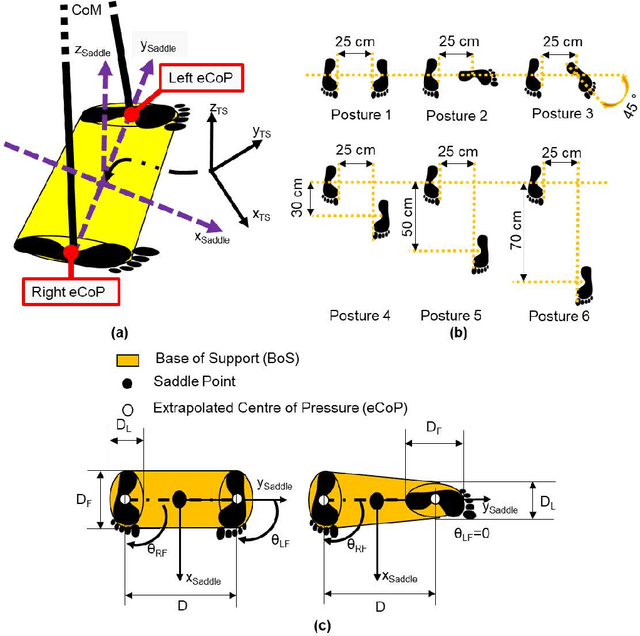
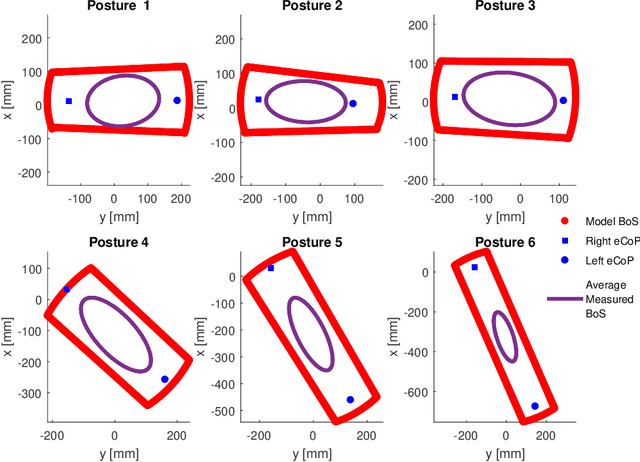
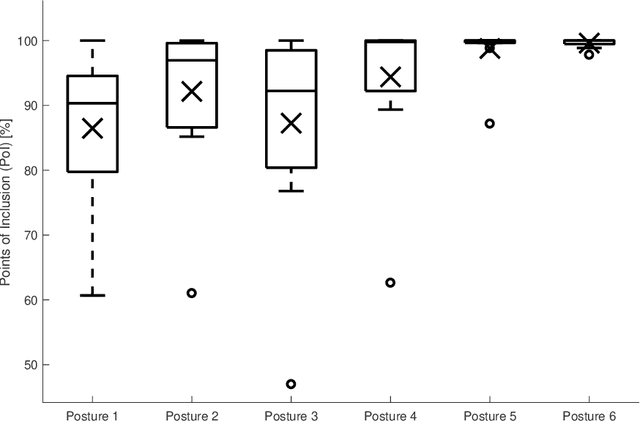
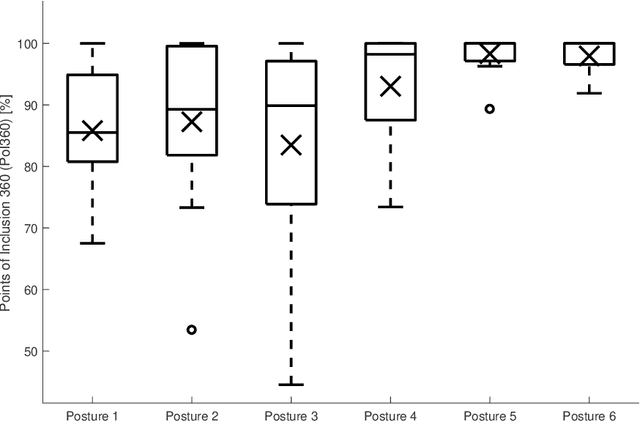
Deployment of the Saddle Space Transformation in Tracking the Base of Support

Balance is the fundamental skill behind human locomotion, and its impairment is the principal indicator of self-perceived disability. Despite significant improvements in balance assessment, there is still large incidence of fall related injuries among elderlies. The Base of Support (BoS) is a popular method for bipedal stability assessment, but its accuracy depends on the accuracy the BoS geometry measurement. This work presents a method to ease the BoS tracking by the identification of a reference frame that allows to define postural models of the BoS geometry. Although we also propose a geometry based on the geometry determined from centre of pressure range of motion within the foot obtained from literature, this methodology can be used with other models (i.e., the feasible base of support). The model has been tested with 12 healthy subjects, which have been asked to explore their stability in six different postures. The results show that the model can accurate deform the geometry of the BoS to adapt its shape to the different postures, which can remove the necessity of force/torque sensors in some application. Potentially the proposed method can be also applied to describe any posture dependent attribute (e.g., gravitational forces), and it can be also applied to bipedal robots. Therefore, it constitutes a novel mathematical tool that can be deployed to develop both better sensors and models for bipeds. For example, it can be used with the Extrapolated CoM model to evaluate dynamic stability from the body kinematics.

The Strange Attractor of Bipedal Locomotion and Consequences on Motor Control

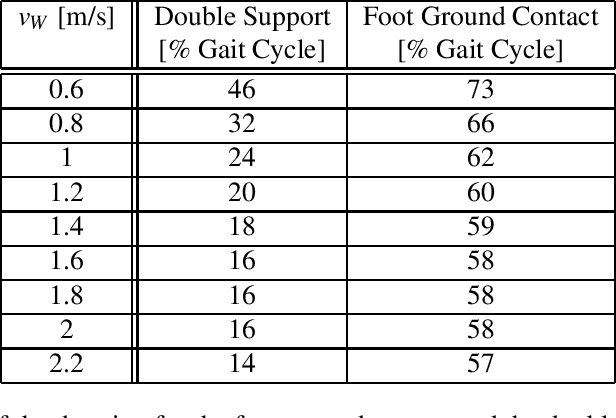
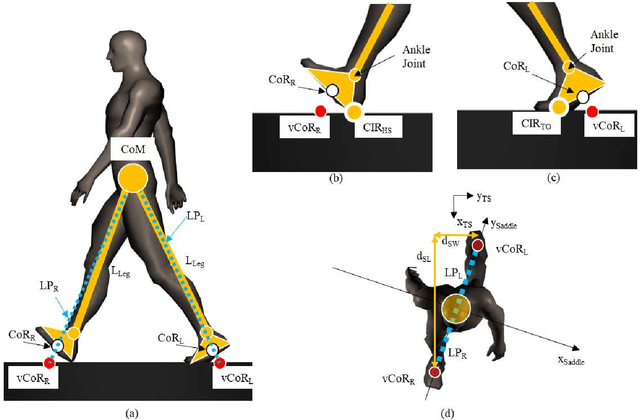
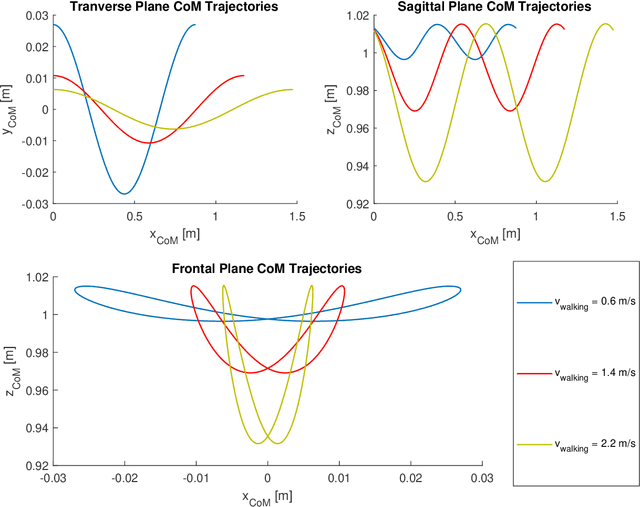
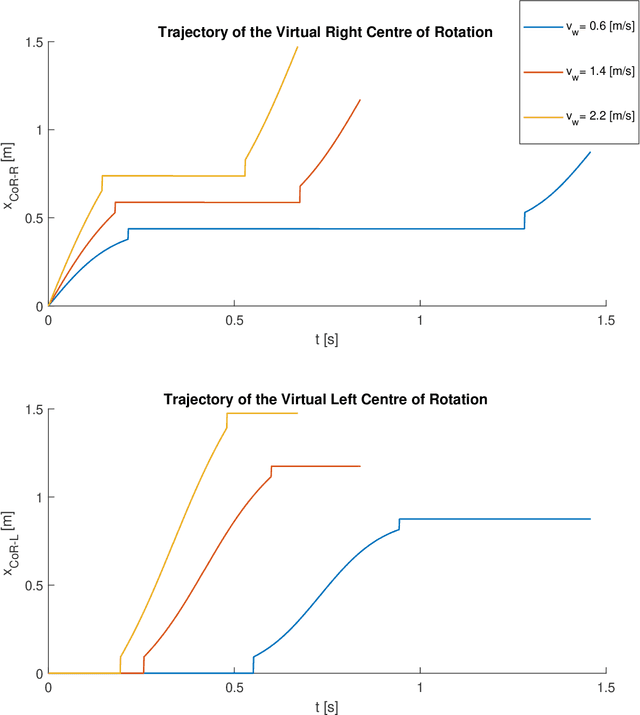
Despite decades of study, the mechanisms that determine human locomotion are still unknown, available models and motor control theories can only partially capture the phenomenon. This is probably the principal cause of the reduced efficacy of lower limbs rehabilitation therapies. Recently, it has been proposed that human locomotion may be planned in the task-space by taking advantage of the gravitational pull acting on the Centre of Mass (CoM) that we have used to formulate a task-space planner for straight locomotion at a constant speed. The proposed model represents the CoM transversal trajectory as simple harmonic oscillator moving forward at a constant speed. On the other hand, the vertical trajectory of the CoM is controlled through the ankle strategies. Our solution is composed of closed-form equations which can plan human-like trajectories for both the CoM and the foot swing. The model output can be seen as the optimal trajectory determined based on the average behaviour of 12 healthy subjects walking at three self-selected speeds. Furthermore, the planner formulation is compatible with an extended formulation of the Passive Motion Paradigm which enables us to design a hierarchical architecture of semi-autonomous controllers. The final architecture can also describe the motor primitives as a particular case of dynamic primitives, shows strong parallels with the nervous system organization, and is compatible with the optimal feedback controller theory.