On Minimal Accuracy Algorithm Selection in Computer Vision and Intelligent Systems

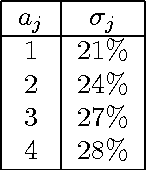
In this paper we discuss certain theoretical properties of algorithm selection approach to image processing and to intelligent system in general. We analyze the theoretical limits of algorithm selection with respect to the algorithm selection accuracy. We show the theoretical formulation of a crisp bound on the algorithm selector precision guaranteeing to always obtain better than the best available algorithm result.

Reasoning and Algorithm Selection Augmented Symbolic Segmentation

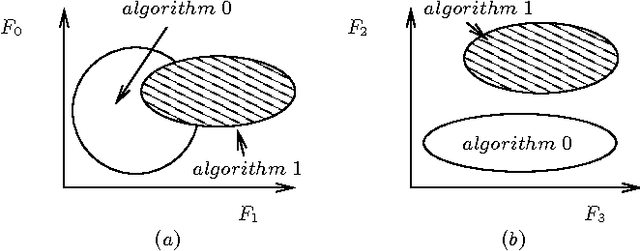
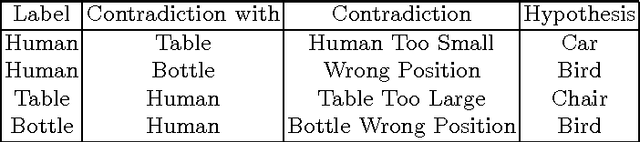
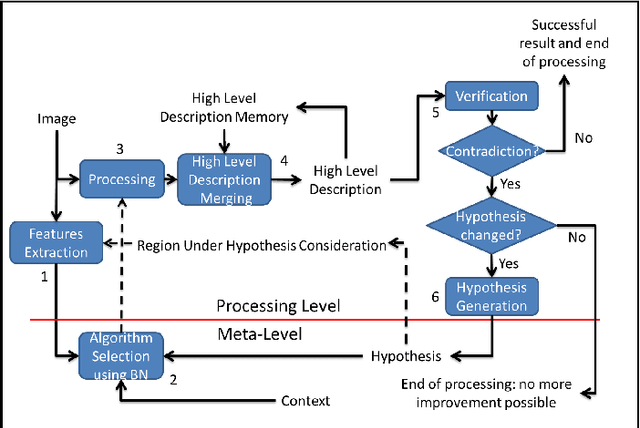
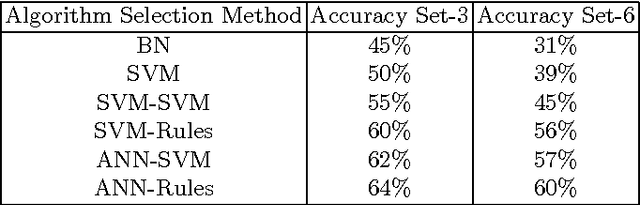
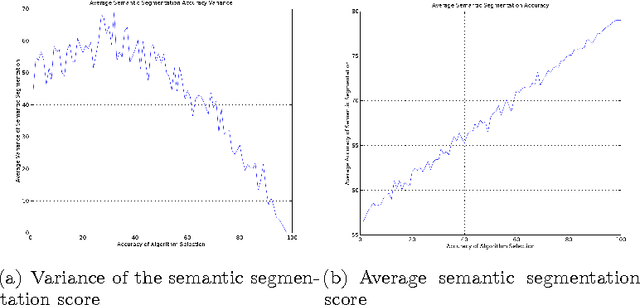
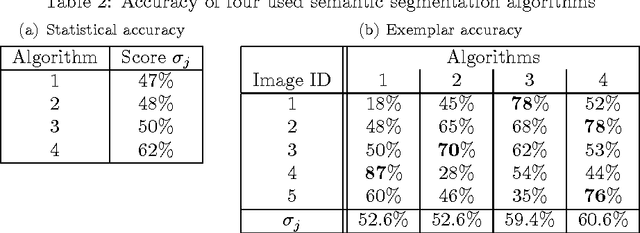
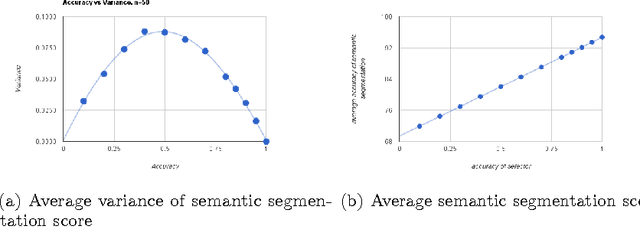
In this paper we present an alternative method to symbolic segmentation: we approach symbolic segmentation as an algorithm selection problem. That is, let there be a set A of available algorithms for symbolic segmentation, a set of input features $F$, a set of image attribute $\mathbb{A}$ and a selection mechanism $S(F,\mathbb{A},A)$ that selects on a case by case basis the best algorithm. The semantic segmentation is then an optimization process that combines best component segments from multiple results into a single optimal result. The experiments compare three different algorithm selection mechanisms using three selected semantic segmentation algorithms. The results show that using the current state of art algorithms and relatively low accuracy of algorithm selection the accuracy of the semantic segmentation can be improved by 2\%.

Symbolic Segmentation Using Algorithm Selection

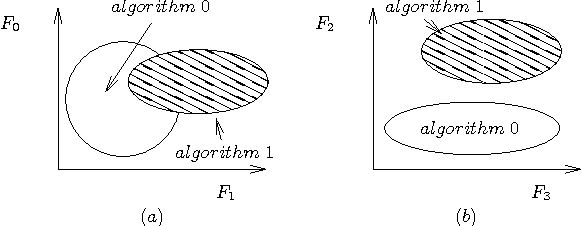
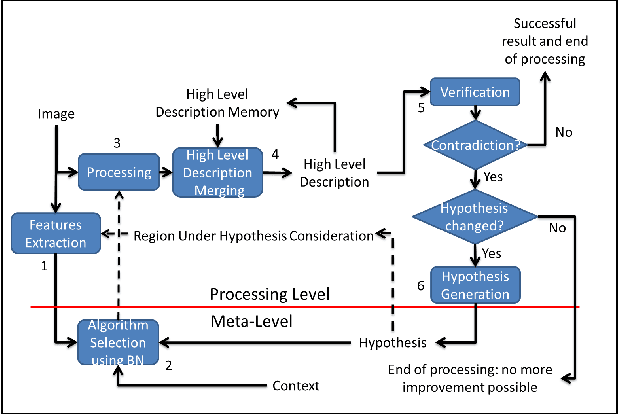
In this paper we present an alternative approach to symbolic segmentation; instead of implementing a new method we approach symbolic segmentation as an algorithm selection problem. That is, let there be $n$ available algorithms for symbolic segmentation, a selection mechanism forms a set of input features and image attributes and selects on a case by case basis the best algorithm. The selection mechanism is demonstrated from within an algorithm framework where the selection is done in a set of various algorithm networks. Two sets of experiments are performed and in both cases we demonstrate that the algorithm selection allows to increase the result of the symbolic segmentation by a considerable amount.

Evolutionary Quantum Logic Synthesis of Boolean Reversible Logic Circuits Embedded in Ternary Quantum Space using Heuristics

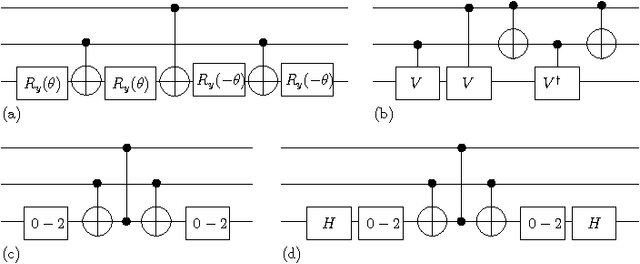
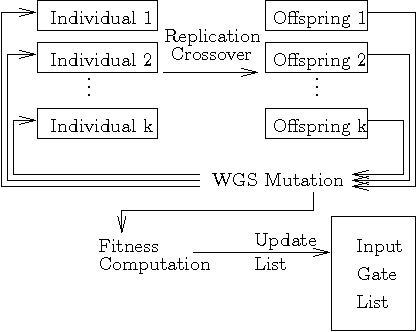
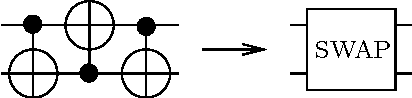
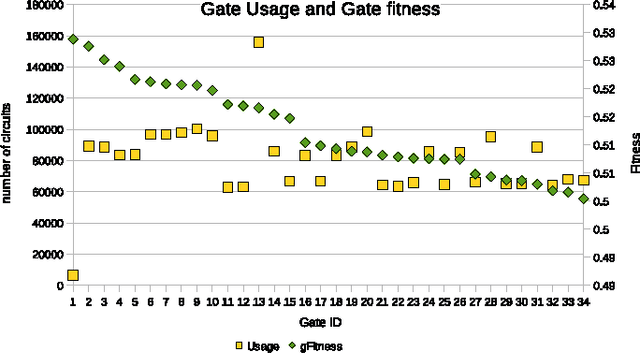
It has been experimentally proven that realizing universal quantum gates using higher-radices logic is practically and technologically possible. We developed a Parallel Genetic Algorithm that synthesizes Boolean reversible circuits realized with a variety of quantum gates on qudits with various radices. In order to allow synthesizing circuits of medium sizes in the higher radix quantum space we performed the experiments using a GPU accelerated Genetic Algorithm. Using the accelerated GA we compare heuristic improvements to the mutation process based on cost minimization, on the adaptive cost of the primitives and improvements due to Baldwinian vs. Lamarckian GA. We also describe various fitness function formulations that allowed for various realizations of well known universal Boolean reversible or quantum-probabilistic circuits.