A Dynamic Approach to Probabilistic Inference

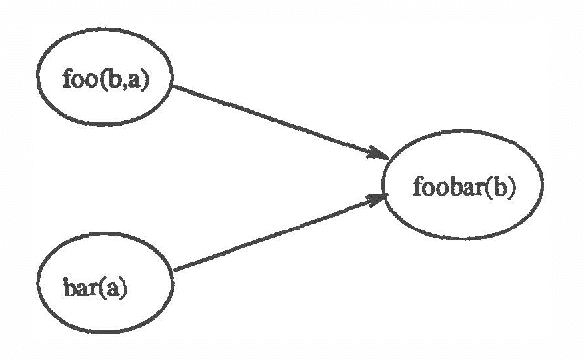
In this paper we present a framework for dynamically constructing Bayesian networks. We introduce the notion of a background knowledge base of schemata, which is a collection of parameterized conditional probability statements. These schemata explicitly separate the general knowledge of properties an individual may have from the specific knowledge of particular individuals that may have these properties. Knowledge of individuals can be combined with this background knowledge to create Bayesian networks, which can then be used in any propagation scheme. We discuss the theory and assumptions necessary for the implementation of dynamic Bayesian networks, and indicate where our approach may be useful.

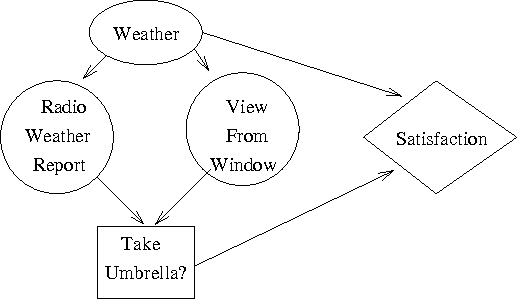
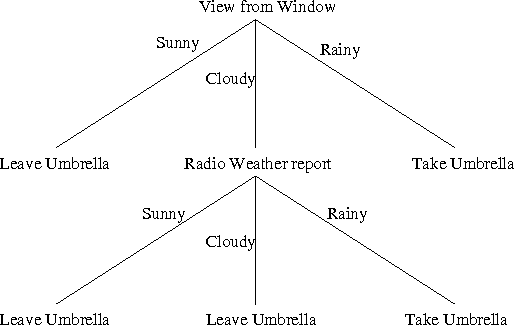
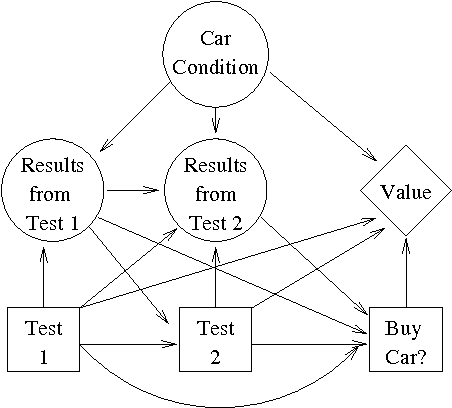
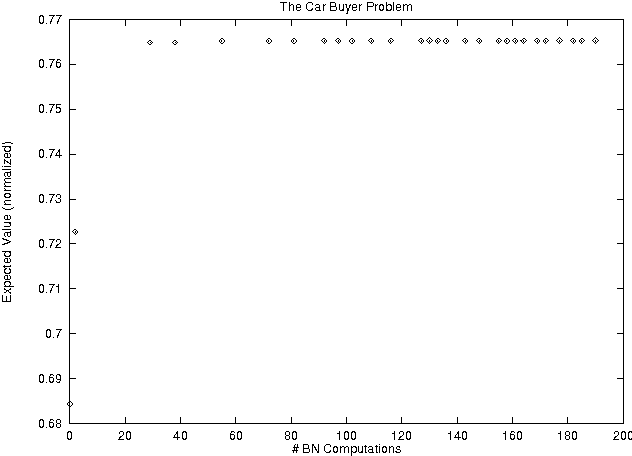
Flexible Policy Construction by Information Refinement

We report on work towards flexible algorithms for solving decision problems represented as influence diagrams. An algorithm is given to construct a tree structure for each decision node in an influence diagram. Each tree represents a decision function and is constructed incrementally. The improvements to the tree converge to the optimal decision function (neglecting computational costs) and the asymptotic behaviour is only a constant factor worse than dynamic programming techniques, counting the number of Bayesian network queries. Empirical results show how expected utility increases with the size of the tree and the number of Bayesian net calculations.

An Anytime Algorithm for Decision Making under Uncertainty

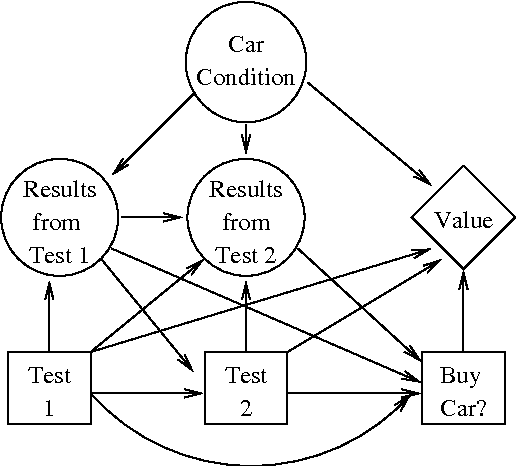
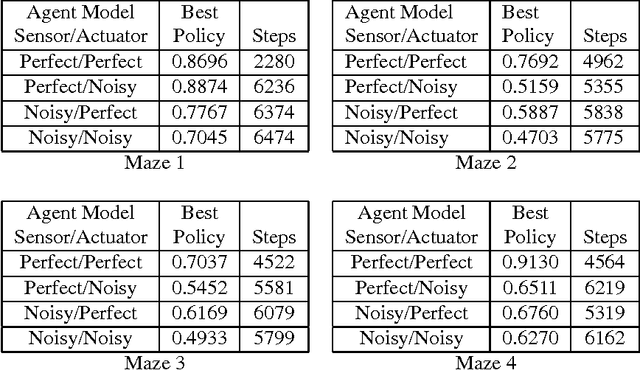
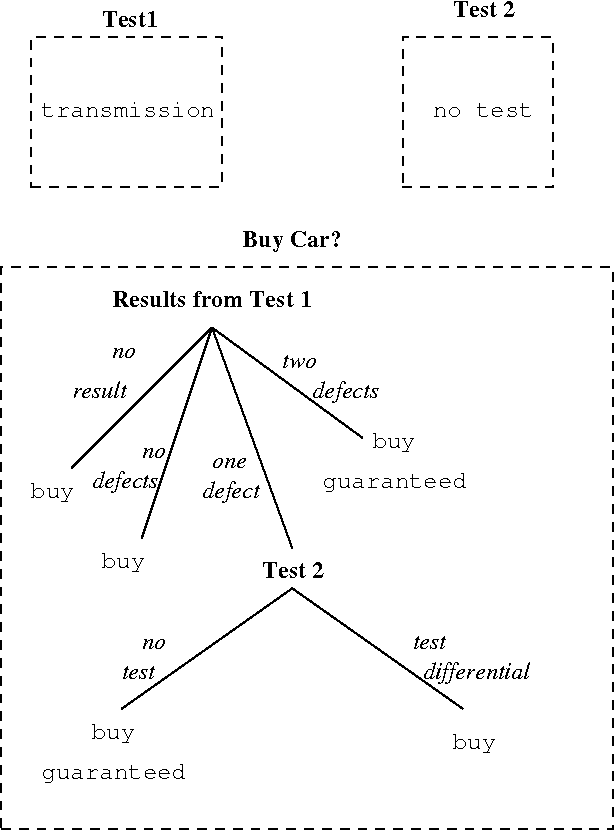
We present an anytime algorithm which computes policies for decision problems represented as multi-stage influence diagrams. Our algorithm constructs policies incrementally, starting from a policy which makes no use of the available information. The incremental process constructs policies which includes more of the information available to the decision maker at each step. While the process converges to the optimal policy, our approach is designed for situations in which computing the optimal policy is infeasible. We provide examples of the process on several large decision problems, showing that, for these examples, the process constructs valuable (but sub-optimal) policies before the optimal policy would be available by traditional methods.

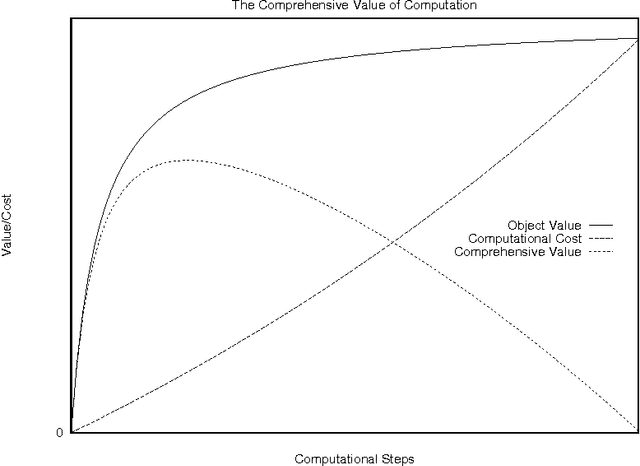
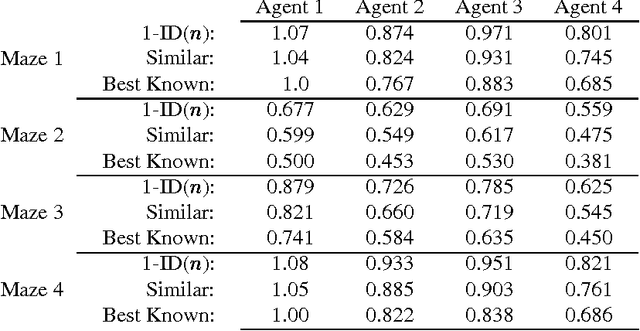
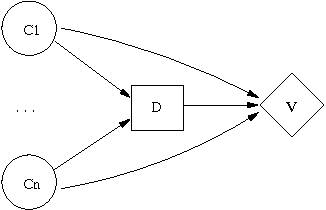
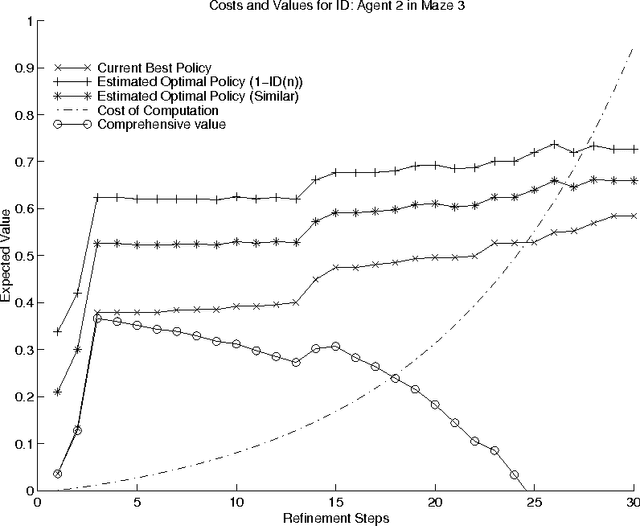
Estimating the Value of Computation in Flexible Information Refinement

We outline a method to estimate the value of computation for a flexible algorithm using empirical data. To determine a reasonable trade-off between cost and value, we build an empirical model of the value obtained through computation, and apply this model to estimate the value of computation for quite different problems. In particular, we investigate this trade-off for the problem of constructing policies for decision problems represented as influence diagrams. We show how two features of our anytime algorithm provide reasonable estimates of the value of computation in this domain.

Probabilistic Arc Consistency: A Connection between Constraint Reasoning and Probabilistic Reasoning

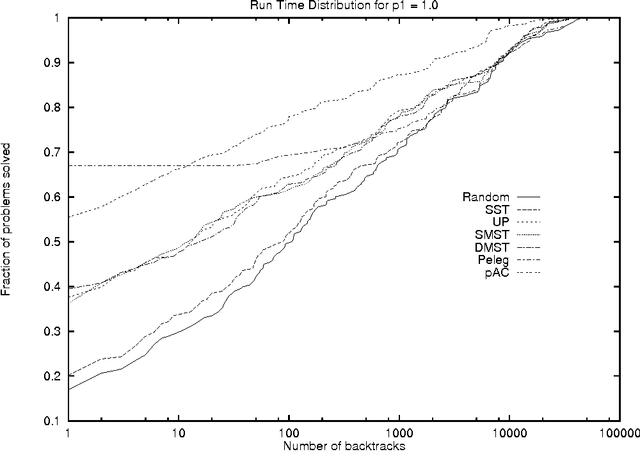
We document a connection between constraint reasoning and probabilistic reasoning. We present an algorithm, called {em probabilistic arc consistency}, which is both a generalization of a well known algorithm for arc consistency used in constraint reasoning, and a specialization of the belief updating algorithm for singly-connected networks. Our algorithm is exact for singly- connected constraint problems, but can work well as an approximation for arbitrary problems. We briefly discuss some empirical results, and related methods.