Mehdi Garrousian
Boundary informed inverse PDE problems on discrete Riemann surfaces
Jun 06, 2022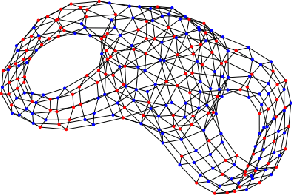
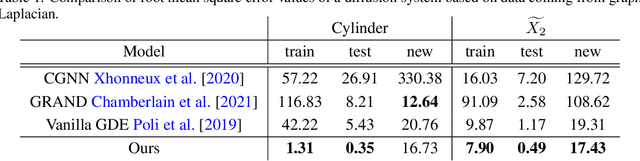

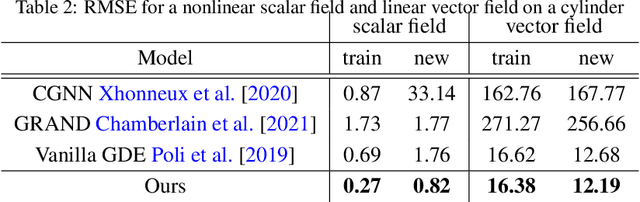
Abstract:We employ neural networks to tackle inverse partial differential equations on discretized Riemann surfaces with boundary. To this end, we introduce the concept of a graph with boundary which models these surfaces in a natural way. Our method uses a message passing technique to keep track of an unknown differential operator while using neural ODE solvers through the method of lines to capture the evolution in time. As training data, we use noisy and incomplete observations of sheaves on graphs at various timestamps. The novelty of this approach is in working with manifolds with nontrivial topology and utilizing the data on the graph boundary through a teacher forcing technique. Despite the increasing interest in learning dynamical systems from finite observations, many current methods are limited in two general ways: first, they work with topologically trivial spaces, and second, they fail to handle the boundary data on the ground space in a systematic way. The present work is an attempt at addressing these limitations. We run experiments with synthetic data of linear and nonlinear diffusion systems on orientable surfaces with positive genus and boundary, and moreover, provide evidences for improvements upon the existing paradigms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge